偏りと参照値のプロット
偏りと参照値のプロットを使用して、各部品で偏り値がどのように異なるかを調べます。青い円は各参照値に対する偏り値を表します。赤い正方形は各参照値に対する平均の偏り値を表します。直線は偏差の平均に適合する最小二乗回帰直線です。
解釈
理想的には、各部品の偏差が0に近く、適合線が水平になります。
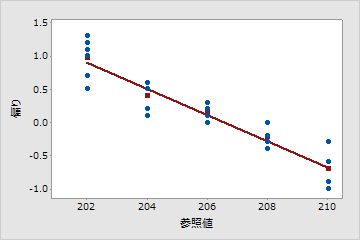
線形性の問題があるように見える
プロットされた線は傾いています。この例では、より小さい部品の測定値は、対応する参照部品の値よりも高いです。より大きい部品の測定値は、対応する参照部品の値よりも低いです。
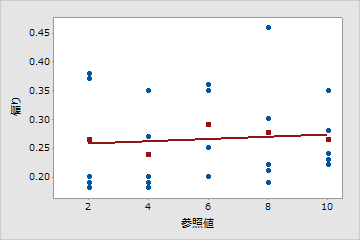
線形性の問題はないように見える
プロットされた線は水平に近く、平均バイアスは相対的に一定で、参照値によって変わることを示しています。この例では、すべての部品の測定値は対応する参照部品の測定値よりも高くなります。
係数
係数は、偏り対参照値プロットの回帰直線から得られる数値です。
この最小二乗回帰直線の一般的な形式は次のようになります。
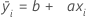
項bは、定数係数を表します。適合線がy軸と交差する位置を示します。
項bは、傾き係数を表します。直線の傾きは、直線の勾配の程度を示し、x軸の変化量に対するy軸の変化量です。
解釈
傾き係数aが非常に小さい場合、傾きは水平に近くなります。したがって、偏りは参照値全体で比較的一定になり、線形性は有意な問題ではありません。傾き係数の絶対値|a|が大きい場合、直線の傾きが急であることを示します。傾きのp値がα未満の場合、線形性が有意です。
有意な線形性が存在せず、定数係数の絶対値|b|が大きい場合、大きな偏りがあることを示します。有意な線形性が存在する場合は、個別の偏り値を調べる必要があります。
係数の標準誤差
回帰係数の推定値の標準誤差は、モデルが係数の未知の値を推定する精度を測定するものです。係数の標準誤差は常に正の値です。
解釈
係数の標準誤差は、係数の推定値の精度を測定するために使用します。標準誤差が小さいほど、推定値は正確です。係数を標準誤差で割ったものがt値です。t値に関連付けられたp値がα水準未満の場合、係数は0とは有意に異なると結論付けます。
ゲージの線形性のp値
- 定数のp値: 線形性直線の定数が0に等しいかどうかを検定するには、これを使用します。
- 傾きのp値: 線形性直線の傾きが0に等しいかどうかを検定するには、これを使用します。
解釈
- 定数に対して、p値がα値より大きい場合、帰無仮説は棄却できず、すべての参照値の偏りは0に等しいと結論付けます。
- 傾きに対して、p値がα値より大きい場合、帰無仮説は棄却できず、すべての参照値(線形性なし)で測定システムの偏りは同じであると結論付けます。
- 定数に対して、p値がα値より小さい場合、帰無仮説を棄却し、すべての参照値の偏りは0に等しくないと結論付けます。
- 傾きに対して、p値がα値より小さい場合、帰無仮説を棄却して、一部の参照値(線形性あり)で測定システムの偏りは同じでないと結論付けます。
SとR二乗
SおよびR二乗(R2)は、モデルがどの程度データに適合するかを示す測度です。
Sは、回帰直線付近の標準偏差σの推定値です。
R二乗(R2)は、偏りと参照値の線形関係で説明される偏りの分散の割合を表します。
解釈
Sが小さいことは、偏りの推定値の変動が小さいことを示します。R2の範囲は0~100%です。通常、R2の値が高くなるほど、モデルのデータ適合度も高まります。
線形性、線形性指標
線形性により、測定システムの予測動作範囲内で平均バイアスの差が評価されます。線形性は、すべての参照値でゲージの精度が同じ(偏りが同じ)かどうかを示します。
線形性指標とは、工程変動におけるパーセントとして表される線形性です。
解釈
データの線形性を解釈するには、偏りが参照値間で変化しているかどうかを特定します。散布図でデータが水平線になっていない場合は、線形性が存在します。適合線が水平で0に近いのが理想的です。

線形性の問題があるように見える
プロットされた線は傾いています。この例では、より小さい部品の測定値は、対応する参照部品の値よりも高いです。より大きい部品の測定値は、対応する参照部品の値よりも低いです。

線形性の問題はないように見える
プロットされた線は水平に近く、平均バイアスは相対的に一定で、参照値によって変わることを示しています。この例では、すべての部品の測定値は対応する参照部品の測定値よりも高くなります。
全部品で測定値が一貫しているゲージでは、線形性指標は0に近くなります。
偏り、偏り度
偏りは、参照部品の既知の標準値と観測された平均測定値の差として計算されます。偏りは、測定システムの正確性の測度です。
偏り度とは、工程変動における偏りのパーセントです。
解釈
- 正の偏りはゲージの測度が高いことを示しています。
- 負の偏りはゲージの測度が低いことを示しています。
ゲージの測定が正確な場合、偏り度も小さくなります。
ゲージの偏りのp値
- 偏りの平均のP: 偏りの平均が0に等しいかどうかを検定するには、これを使用します。
- 各参照値のP: 各参照値で偏りが0に等しいかどうかを検定するには、これを使用します。
解釈
- 各参照値に対して、p値がα値より大きい場合、帰無仮説は棄却できず、偏りは0に等しいと結論付けます。
- 偏りの平均に対して、p値がα値より大きい場合、帰無仮説を棄却できず、偏りの平均は0に等しいと結論付けます。
- 各参照値に対して、p値がα値より小さい場合、帰無仮説を棄却し、偏りは0に等しくないと結論付けます。
- 偏りの平均に対して、p値がα値より小さい場合、帰無仮説を棄却し、偏りの平均は0に等しくないと結論付けます。
