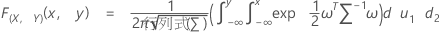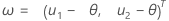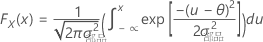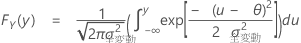ゲージR&R拡張分析法
Minitabでは、ランダム効果モデル、混合効果モデル、および枝分かれ計画モデルの3つの分散分析モデルを使用して一般線形モデル手法によりゲージR&R分析を実行します。ランダム効果モデルがデフォルトです。いずれかの因子が固定または枝分かれの場合には混合効果モデルまたは枝分かれ計画モデルが使用されます。
最終的に選択されるモデルには、主効果項、有意な高次の交互作用、およびその間の関連する交互作用のみが含まれます。Minitabにより適切なモデルの分散分析表が計算されます。その後、この表を使用して分散成分が計算され、分散成分はゲージR&R表に表示されます。
参考文献
Burdick, R. K., Borror, C. M., and Montgomery, D.C. (2003). "A Review of Methods for Measurement Systems Capability Analysis", Journal of Quality Technology, 35(4) 342–354.
Adamec, E. and Burdick, R.K. (2003). "Confidence Intervals for a Discrimination Ratio in a Gauge R&R Study with Three Random Factors", Quality Engineering, 15(3) 383–389.
ランダム効果モデル
このコマンドで使用されるデフォルトのモデルはランダム効果モデルです。3因子の完全モデルを指定した場合、次のようになります。
Yijkl = μ + Pi + Oj + Ak + (PO)ij + (PA)jk + (OA)jk + (POA)ijk + εijkl
| 用語 | 説明 |
|---|---|
| μ | 定数 |
| Pi | i番目の部品 |
| 用語 | 説明 |
|---|---|
| Oj | j番目の測定者 |
| 用語 | 説明 |
|---|---|
| Ak | 追加因子のk番目の水準 |
Pi、Oj 、Ak、 (PO)ij、 (PA)jk、 (OA)jk、 (POA)ijk、およびεijkl は、それぞれ独立して正規分布に従っており、平均は0で分散はそれぞれ次のようになります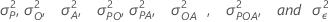 .
.
Minitabでは、一般線形モデルの適合を使用して分散成分を推定します。分散成分の推定の詳細は、「一般線形モデルの適合の方法と計算式」を参照してください。
- 合計ゲージR&R
-

- 繰り返し性
-

- 再現性
-
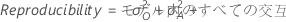
- 作業者
-

- A
-

- 部品*測定者
-

- 部品 * A
-

- 部品間
-

- 部品
-

- 全変動
-
注
工程変動を推定するために過去の標準偏差を指定して使用するときは以下を行います。
- 過去の標準偏差が、データから算出されたゲージの標準偏差の合計よりも大きい場合、標準偏差の合計はσであり、部品間の標準偏差は次の通りです。
 .
. - 他方、Minitabではデータを使用して標準偏差の合計と部品間の変動を推定します。
- 合計ゲージR&R
-

- 繰り返し性
-

- 再現性
-
- 作業者
-

- 部品*測定者
-

- 部品間
-

- 部品
-

- A
-

- 部品 * A
-

- 全変動
-
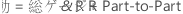
注
工程変動を推定するために過去の標準偏差を指定して使用するときは以下を行います。
- 過去の標準偏差が、データから算出されたゲージの標準偏差の合計よりも大きい場合、標準偏差の合計はσであり、部品間の標準偏差は次の通りです。
 .
. - 他方、Minitabではデータを使用して標準偏差の合計と部品間の変動を推定します。
- ゲージの繰り返し性 = 誤差項の分散成分
- 部品間の変動 = 部品の分散成分、または部品間項の分散成分の和
- ゲージの再現性 = 残りの項の分散成分の和
混合効果モデル
線形モデルの一部の項が固定の場合、それは混合効果モデルになります。変量項の分散成分は一般線形モデルの適合の結果を使用して得られます。
分散成分の推定の詳細は、「一般線形モデルの適合の方法と計算式」を参照してください。
- 線形モデルを当てはめることにより、因子の最初のJ-1個の水準の係数が推定されます。
- 水準Jの係数 = -(最初のJ-1個の水準の係数の和)
- 推定される変動性 = すべての水準の(係数)2の和 / 水準数
混合効果のゲージ再現性の計算では、固定項の分散成分はφに置き換えられますが、ランダム効果モデルの定義は保持されます。
枝分かれ計画モデル
一部の因子が他の因子の下で枝分かれしている場合、Minitabでは一般線形モデルの適合を使用してモデルを当てはめます。分散成分の推定の詳細は、「一般線形モデルの適合の方法と計算式」を参照してください。
ゲージの繰り返し性、再現性、および部品間変動は、変量因子および固定因子の場合と同様に定義されます。
ゲージR&R(拡張)の計算
Minitabでは拡張ゲージR&R分析に2つの表が表示されます。最初の表には分散成分列と(分散成分の)寄与度列が含まれています。分散成分の推定の詳細は、「一般線形モデルの適合の方法と計算式」を参照してください。
寄与度 = 分散成分の値 / 全変動
- 標準偏差(SD) = sqrt(分散成分)
- 基準変動 = 標準偏差の数*標準偏差
- %基準変動(%SV) = 基準変動 / 全変動の基準変動
- %公差 = 基準変動 / 工程公差
- %工程 = 標準偏差 / 標準偏差の経験値
%公差と信頼区間
%公差とは、各成分の公差のパーセントです。
公差(上側規格限界 - 下側規格限界)が指定されると、各成分の基準変動を指定された公差で割ることによって%公差が計算されます。
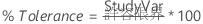
1つの規格限界のみ指定した場合、公差は各成分の基準変動の半分を片側許容限界で割った値になります。片側許容限界は、指定された規格限界の絶対値を、すべての測定値の平均から差し引いた値です。
この値は、工程公差(上側規格 – 下側規格)またはオプションサブダイアログボックスに規格限界を入力した場合にのみ表示されます。
LとUが分散成分の下限と上限である場合、対応する公差の信頼区間は次のようになります:

| 用語 | 説明 |
|---|---|
| k | kは分析定数で、デフォルト値は6です |
知覚区分数
知覚区分数は、製品変動の範囲内にある重複していない信頼区間の数を表します。これはまた、使用中の測定システムが工程データ内で識別できるグループ数と考えることもできます。

次に、この値が切り捨てられます。ただし、値が1未満になる場合、知覚区分数は1に設定されます。
信頼区間
LとUがゲージ分散と合計分散の比の下限と上限だとすると、知覚区分数の下限と上限は次のようになります。


注
LとUは(0,1)の範囲内にある必要があります。LとUが範囲外にある場合、知覚区分数の下限と上限は欠損します。
誤判別確率
Minitabでは、1つ以上の規格限界を入力すると、同時確率と条件付き確率の両方の誤判別確率が計算されます。分散分析法とXbar-R法を使用する分析の場合、結果には分散分析法を使用した場合の誤分類の確率が含まれます。
同時確率
不良品を合格と判別する確率
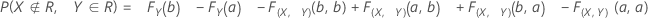
良品を不合格と判別する確率

条件付き確率
不良品を合格と判別する確率(誤った合格)

良品を不合格と判別する確率(誤った不合格)

表記
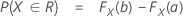
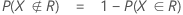
F(X,Y)は、2変量正規確率ベクトル(X,Y)T の累積分布関数(CDF)で、
その平均μ = (θ,θ)Tです。

F(X)とF(Y)は、対応する周辺CDFです。
つまり、