ある工程エンジニアが、ガラス製造工程のガラス屈折測定システムを評価したいと考えています。エンジニアの依頼により3人の測定者が22個のガラス部品の屈折特性を2つの作業場所で測定します。
この分析には固定因子(作業場所)があるため、エンジニアは拡張ゲージR&R分析を実行し、測定システムで発生している可能性がある測定値の変動を評価します。
- サンプルデータガラス屈折.MWXを開きます。
- を選択します。
- 部品番号に部品を入力します。
- 測定者に測定者を入力します。
- 測定データに測定値を入力します。
- 追加因子に測定場所を入力します。
- 固定因子に測定場所を入力します。
- 項ボタンをクリックします。
- モデルに含める項の次数から[2]を選択します。
- 選択された項で、部品*測定場所の交互作用項をモデルから削除します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
最初の二元配置分散分析表は、部品、測定者、固定因子、および交互作用の項を含みます。交互作用のp値が0.05以上の場合は有意ではないため、Minitabではその交互作用が完全モデルから除外されます。この例では、測定者*部品のp値は0.189で、測定者*測定場所のp値は0.598です。そのため、最終モデルからこれらの交互作用を除外した2番目の二元配置分散分析表が生成されます。
屈折データの場合、測定システム(合計ゲージR&Rの寄与率が約49%)には部品(部品間の寄与度が約51%)と同程度の変動があります。合計ゲージR&Rは基準変動の約70%です。繰り返し性は基準変動の約69%で、これは測定システムが同じ部品を一貫して測定していないことを示しています。
この工程の知覚区分数は1しかなく、これは測定システムが部品を区別できないことを示しています。詳細は、ゲージR&R分析における異なるカテゴリの数の使用を参照してください。
グラフから、測定システムに関する次の情報も得られます。
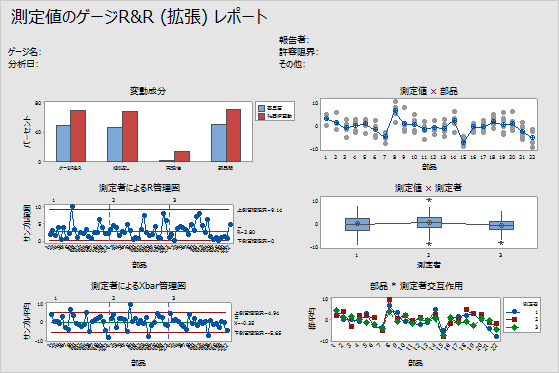
- 変動成分グラフから、測定システムによって説明される変動量が部品間の変動量と同じぐらいあることが分かります。特に、変動のほとんどは、測定システムの不正確さ(繰り返し性)によるものです。
- 測定者別R管理図では、いくつかのデータ点は管理外にあり、これは、3人の測定者の測定に一貫性がないことを示しています。
- 測定者別Xbar管理図では、各測定者に対して、いくつかの点のみが管理限界を超えています。この管理図では、許容できる測定システムを示すには50%以上の点が管理外にある必要があります。したがって、この例では、Xbar管理図は測定システムを許容できない可能性を示しています。
- 部品別グラフでは、各部品の測定値が明らかに異なります。この変動性は測定システムの不正確さに起因する可能性があります。平均間にも明らかに差があります。分析に使用される部品は可能な部品の範囲全体を代表するべきであるため、これは望ましい状態です。
- 測定者別グラフでは、各測定者の測定値の変動量がほぼ同じです。いくらかの変動は常に存在しますが、データは、測定者が同様に測定していることを示しています。
- 測定者*部品の交互作用グラフでは、線が互いに近くなっています。ただし、一貫性がない部分もあります。たとえば、測定者3の部品19に対する測定値は他の2名の測定者と差があるように見えます。
因子情報
| 因子 | タイプ | 水準 | 値 |
|---|---|---|---|
| 部品 | ランダム | 22 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 |
| 測定者 | ランダム | 3 | 1, 2, 3 |
| 測定場所 | 固定 | 2 | 1, 2 |
分散分析表 (すべての項)
| 要因 | 自由度 | 逐次平方和 | 調整平方和 | 調整平均平方 | F値 | p値 | |
|---|---|---|---|---|---|---|---|
| 部品 | 21 | 1071.30 | 1071.30 | 51.014 | 6.46 | 0.000 | |
| 測定者 | 2 | 32.18 | 32.18 | 16.089 | 3.27 | 0.164 | x |
| 測定場所 | 1 | 11.25 | 11.25 | 11.247 | 3.50 | 0.202 | |
| 部品*測定者 | 42 | 331.81 | 331.81 | 7.900 | 1.27 | 0.189 | |
| 測定者*測定場所 | 2 | 6.43 | 6.43 | 3.217 | 0.52 | 0.598 | |
| 繰り返し性 | 63 | 390.53 | 390.53 | 6.199 | |||
| 合計 | 131 | 1843.50 |
分散分析 (ANOVA) 表 (ゲージR&R計算に使用した項付き)
| 要因 | 自由度 | 逐次平方和 | 調整平方和 | 調整平均平方 | F値 | p値 |
|---|---|---|---|---|---|---|
| 部品 | 21 | 1071.30 | 1071.30 | 51.014 | 7.49 | 0.000 |
| 測定者 | 2 | 32.18 | 32.18 | 16.089 | 2.36 | 0.099 |
| 測定場所 | 1 | 11.25 | 11.25 | 11.247 | 1.65 | 0.202 |
| 繰り返し性 | 107 | 728.77 | 728.77 | 6.811 | ||
| 合計 | 131 | 1843.50 |
分散成分
| 要因 | 分散成分 | (分散成分の)寄与度 |
|---|---|---|
| 合計ゲージR&R | 7.1070 | 49.10 |
| 繰り返し性 | 6.8109 | 47.06 |
| 再現性 | 0.2961 | 2.05 |
| 測定者 | 0.2109 | 1.46 |
| 測定場所 | 0.0852 | 0.59 |
| 部品間 | 7.3672 | 50.90 |
| 部品 | 7.3672 | 50.90 |
| 全変動 | 14.4743 | 100.00 |
ゲージ評価
| 要因 | 標準偏差 (SD) | 基準変動 (6×SD) | %基準変動(%SV) |
|---|---|---|---|
| 合計ゲージR&R | 2.66590 | 15.9954 | 70.07 |
| 繰り返し性 | 2.60978 | 15.6587 | 68.60 |
| 再現性 | 0.54413 | 3.2648 | 14.30 |
| 測定者 | 0.45921 | 2.7552 | 12.07 |
| 測定場所 | 0.29189 | 1.7514 | 7.67 |
| 部品間 | 2.71427 | 16.2856 | 71.34 |
| 部品 | 2.71427 | 16.2856 | 71.34 |
| 全変動 | 3.80450 | 22.8270 | 100.00 |
識別区分数 = 1