このトピックの内容
分散成分
分散成分の寄与度プロットと分散成分表には、さまざまな要因からの変動が表示されます。
解釈
分散成分を使用して、各ソースからの変動を評価します。検定-再検定分散と測定者分散は測定誤差です。部品変動は、分析における部品の範囲を表します。合計分散は、他の成分の合計です。分析に交互作用が含まれる場合、測定誤差の量は、測定者が測定する部品によって異なります。
許容可能な測定システムでは、ばらつきの最大の成分は部品のばらつきです。テストと再テストのばらつきおよび測定者のばらつきが大きなばらつきに寄与している場合は、問題の原因を調査し、修正処置を行ってください。
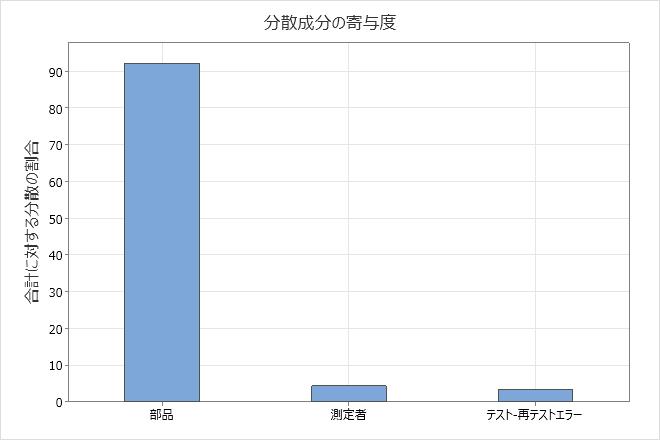
分散成分
| 要因 | 分散 | %合計 | 標準偏差 |
|---|---|---|---|
| テスト-再テストエラー(繰り返し性) | 0.03997 | 3.394 | 0.19993 |
| 測定者(再現性) | 0.05146 | 4.368 | 0.22684 |
| 部品(製品変動) | 1.08645 | 92.238 | 1.04233 |
| 合計 | 1.17788 | 100.000 | 1.08530 |
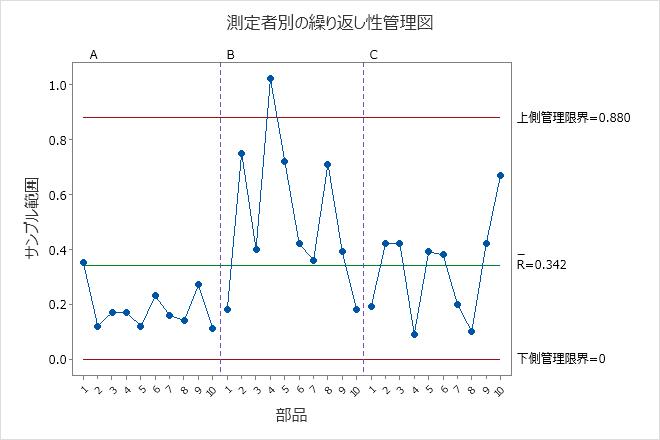
繰り返し性管理図
繰り返し性管理図は、測定者の一貫性を示す範囲の管理図です。
- プロットされた点
- 各測定者のサンプル範囲は、各部品の最大測定値と最小測定値の差です。サンプル範囲を使用して、演算子の一貫性を評価します。
- 中心線(Rbar)
- 工程の全体平均(つまり、すべてのサンプル範囲の平均)。
- 管理限界(LCLとUCL)
- サンプル範囲の期待変動量。管理限界を計算するために、Minitabではサンプル内の変動が使用されます。
注
各測定者が各部品を9回以上測定すると、範囲ではなく標準偏差が管理図に表示されます。
解釈
平均範囲が小さいほど、測定システムからの変動は小さくなります。点が上側管理限界(UCL)を超えている場合は、測定者が部品を一貫して測定していないことを示します。UCLの計算には、各測定者による部品ごとの測定数と部品のばらつきが含まれます。測定者が部品を一貫して測定している場合は、最大測定値と最小測定値の範囲が、基準変動と比較して小さくなり、点は管理下にあります。
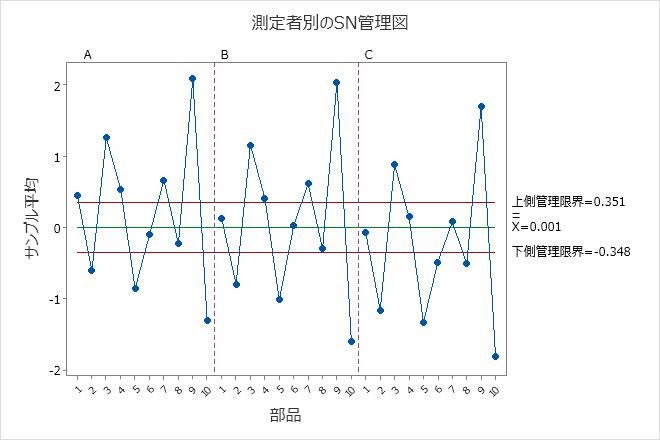
測定者別のSN管理図
このグラフは、部品のばらつきをテストと再テストのコンポーネントと比較します。
- プロットされた点
- 各測定者がプロットした部品ごとの平均測定値。
- 中心線 (
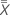 )
) - すべての測定者によるすべての部品の測定値の全体平均。
- 管理限界(LCLとUCL)
- 臨界距離は繰り返し性の測定値と平均ごとの測定値の数に基づいています。
解釈
スタディ用に選択される部品は、可能な部品の全範囲を表す必要があります。したがって、このグラフは、試験と再試験のばらつきのみから予想される変動よりも、部品平均間の変動が大きいことを示しているはずです。
グラフに、低い分散を持つ測定システムがあることを示す臨界の範囲外の点が多く、臨界距離が狭いのが理想的です。
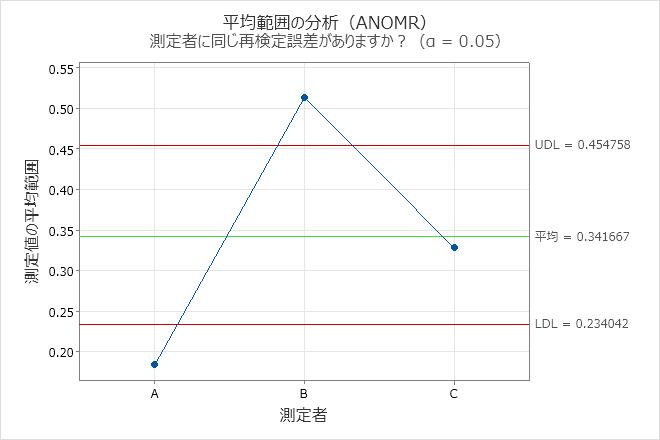
並列性管理図
平行度プロットには、各部品の各測定者による平均測定値が表示されます。各線は、単一作業者の平均値をつないでいます。
プロットには、部品と測定者という2つの変動要因間の交互作用が表示されます。交互作用は、ある因子の効果は第2因子に依存する場合に発生します。
解釈
線が一致する場合、測定者の測定値が類似していることを示します。平行でない線や交差している線は、測定者が部品を一貫して測定する能力が、どの部品を測定するかによって異なることを示します。他の線よりも一貫して高いまたは低い線は、測定者が一貫して高くまたは低く測定していることにより、測定値に偏りが加わっていることを示します。
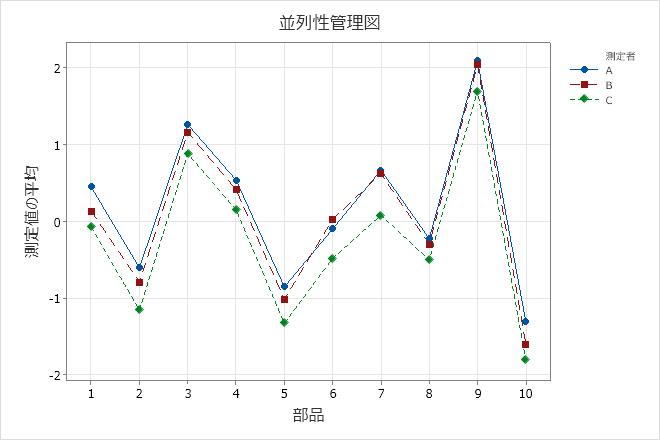
主効果の分析(ANOME)プロット
このプロットでは、測定者の平均測定値が比較されます。
- プロットされた点
- 各測定者のすべての部品の平均測定値。
- 中心線 (平均)
- すべての測定者によるすべての部品の測定値の全体平均。
- 決定限界(LDLおよびUDL)
- 限界は、検定-再検定推定値と各平均の測定値数に基づきます。
解釈
決定限界の外側の点は、異なる測定者が測定値に偏りを加えていることを示します。理想的には、すべての点が決定限界内にあり、測定者の全体平均が類似していることを示します。
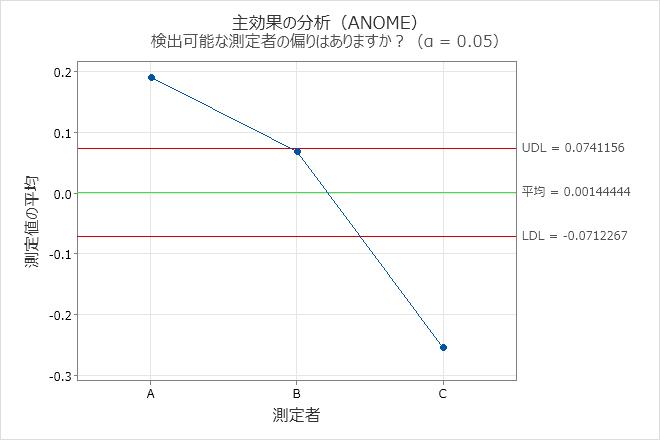
平均範囲の分析(ANOMR)プロット
このプロットでは、測定者の平均測定範囲が比較されます。
- プロットされた点
- 各測定者の各部品の測定値の範囲の平均。
- 中心線 (平均)
- すべての演算子によるすべての範囲の全体的な平均。
- 決定限界(LDLおよびUDL)
- 制限は、テストと再テストの推定値に基づいています。
解釈
決定限界の外側の点は、一部の測定者が他の測定者よりも多かれ少なかれ一貫して測定していることを示します。理想的には、測定者の全体的な範囲が類似していることを示すために、すべての点が決定限界内にあります。
EMP統計量と分類のガイドライン
EMP統計量は、測定システムをファーストクラスの最高の評価から4クラスの最悪の評価に分類します。クラスは、クラス内相関係数に対応します。実際には、係数は、測定システムが少なくとも3標準偏差の工程平均のシフトをどの程度検出するかを説明します。第1級および第2級の測定システムは、通常、管理図上の限られた数の検定とサブグループで、このようなシフトを検出する確率が高くなります。第3クラスの測定システムでは、標準的な分析で管理図に検定が追加され、工程平均のシフトを検出する確率が高まります。第4クラスの測定システムは、通常、プロセスの監視またはプロセス改善活動のために改善が必要です。
この分類は、プロセスからの信号の減衰にも関連しています。減衰は、測定誤差と交絡する変化の量です。変化の50%を減衰させる測定システムの場合、2標準偏差の変化は1標準偏差の変化として現れる可能性があります。
- テスト-再テストエラー
- 同じ測定者が同じ部品を複数回測定した場合の測定値のばらつき。値が小さいほど、測定システムのパフォーマンスは向上します。
- 自由度
- 検定-再検定誤差を推定するための自由度 (DF)。一般に、DFは誤差の計算に利用できる情報量を測定します。
- 確率誤差
- 1回の測定の不確実性。この分析では、推定誤差を測定の有効分解能テーブルの測定増分と比較し、測定の精度が信頼できるかどうかを結論付けます。Wheeler (2006) 1 測定システムの性能を前提として、推定誤差を使用して工程の規格限界を決定する方法について説明します。
- 組内相関
- 組内相関係数は、全体の変動と部品の変動を比較します。値が 1 に近いほど、測定システムからの変動が少ないことを示します。
- 偏りなし
- 偏りがない場合、係数は、すべての測定者が平均して同じ部品を測定した場合の測定システムのパフォーマンスを表します。
- 偏りあり
- 偏りありでは、係数は測定者間の差で測定システムがどの程度うまく機能するかを表します。
- 偏りと相互作用あり
- 分析によって、測定者によって部品の測定方法が異なることが検出された場合、結果にはバイアスと交互作用によるクラス内相関が含まれます。係数は、測定者によって部品の測定が異なる場合の測定システムの性能を表します。
- 偏りの影響
- 偏りのあるクラス内係数と偏りなしのクラス内係数の差。値が小さいほど、測定者の違いが測定値の変動に寄与することは少なくなります。
- 偏りと相互作用の影響
- 偏りありと交互作用のあるクラス内係数と偏りありのない係数の差。値が小さいほど、異なる測定者によるさまざまな部品の測定方法の違いが測定値の変動に寄与することは少なくなります。
EMP統計量
| 統計量 | 値 | 分類 |
|---|---|---|
| テスト-再テストエラー | 0.1999 | |
| 自由度 | 78.0000 | |
| 確率誤差 | 0.1349 | |
| 組内相関(偏りなし) | 0.9645 | 第1組 |
| 組内相関(偏りあり) | 0.9224 | 第1組 |
| 偏りの影響 | 0.0421 |
分類ガイドライン
| 分類 | 組内相関 | プロセス信号の減衰 | 警告の確率、テスト1* | 警告の確率、テスト* |
|---|---|---|---|---|
| 第1組 | 0.80 - 1.00 | 11%未満 | 0.99 - 1.00 | 1.00 |
| 第2組 | 0.50 - 0.80 | 11 - 29% | 0.88 - 0.99 | 1.00 |
| 第3組 | 0.20 - 0.50 | 29 - 55% | 0.40 - 0.88 | 0.92 - 1.00 |
| 第4組 | 0.00 - 0.20 | 55%超 | 0.03 - 0.40 | 0.08 - 0.92 |
測定値の効果的な分解能
分解能に関する統計は、記録された測定値の精度をどの程度信頼できるかを示します。
- 確率誤差(PE)
- 1回の測定の不確実性。この分析では、推定誤差を測定の有効分解能テーブルの測定増分と比較し、測定の精度が信頼できるかどうかを結論付けます。Wheeler(2006)1 は、測定システムの性能を前提として、推定誤差を使用して工程の規格限界を決定する方法を説明しています。
- 増分の下限(0.1 * PE)
- 測定増分が信頼できる場合の下限。測定増分が増分の下限より小さい場合は、測定値の精度を低く記録するかどうかを強く検討してください。
- 最小有効増分(0.22 * PE)
- システムが生成する可能性のある測定値の精度の推定値。測定増分が最小有効増分より小さい場合は、測定値の記録精度を低くするかどうかを検討します。
- 現在の測定増分
- データからの推定値、または記録された測定値の精度を説明する指定された値。たとえば、値1.1、1.4、および1.9の場合、測定値には10分の1の位置が含まれているため、増分は0.1であると判断されます。
- 最大有効増分(2.2 * PE)
- システムが生成する可能性のある測定値の精度の推定値。測定増分が最大有効増分よりも大きい場合は、測定値をより高い精度で記録するかどうかを検討します。
誤判別確率
1つ以上の規格限界を指定すると、製品の誤判別確率を計算できます。ゲージは変動するため、部品を測定した値は、部品の真の値と常に一致するわけではありません。測定値と実際の値の相違は、部品の誤判別につながる可能性があります。
- 同時確率
- 部品を許容できるかどうかについて事前の情報がない場合は、同時確率を使用します。たとえば、ラインからサンプル抽出を行うときに各部品が良好であるか不良であるかが分からない場合です。次の2つの誤判別が起こり得ます。
- 不良品を合格と判別する確率
- 良品を不合格と判別する確率
- 条件付き確率
- 部品を許容できるかどうかについて事前の情報がある場合、条件付き確率を使います。たとえば、再加工対象の製品群からサンプル抽出を行ったり、良品として出荷する予定の製品群からサンプル抽出を行う場合です。次の2つの誤判別が起こり得ます。
- 再加工が必要な不良品群からサンプル抽出された部品を合格と判別する確率(誤った合格)
- 出荷予定の良品群からサンプル抽出された部品を不合格と判別する確率(誤った不合格)
解釈
誤分類の同時確率
| 説明 | 確率 |
|---|---|
| ランダムに選んだ部品が不良品でも合格 | 0.037 |
| ランダムに選んだ部品が良品でも不合格 | 0.055 |
誤分類の条件付き確率
| 説明 | 確率 |
|---|---|
| 不良品グループ内の部品が合格 | 0.151 |
| 良品グループ内の部品が不合格 | 0.073 |
不良品を合格と判別する同時確率は0.037です。良品を不合格と判別する同時確率は0.055です。
実際は規格外の部品を再検査で合格と判別する誤った合格の条件付き確率は0.151です。実際は規格内の部品を再検査で不合格と判別する誤った不合格の条件付き確率は0.073です。
