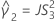
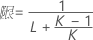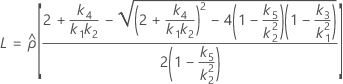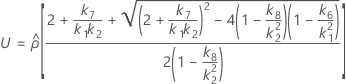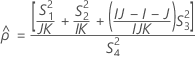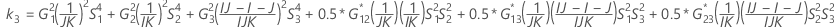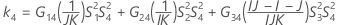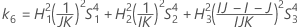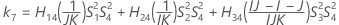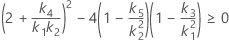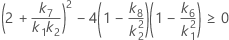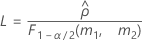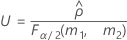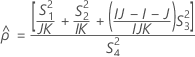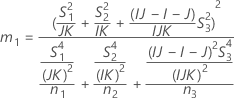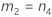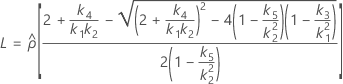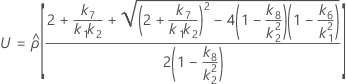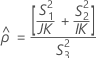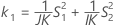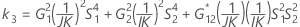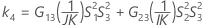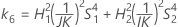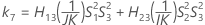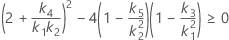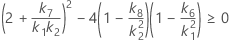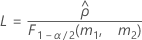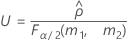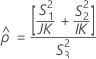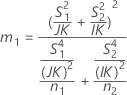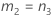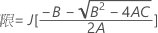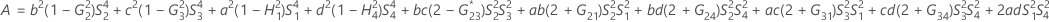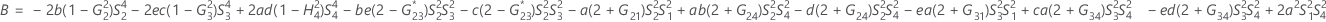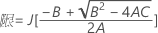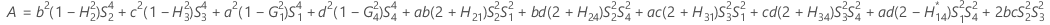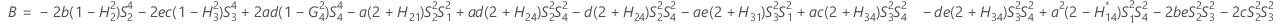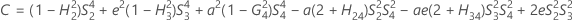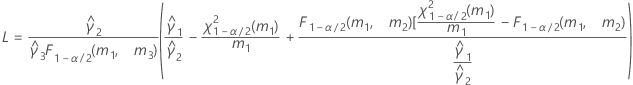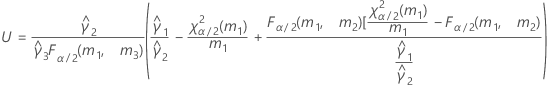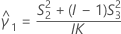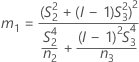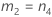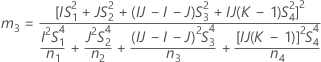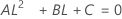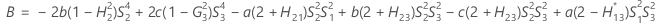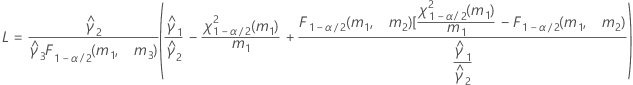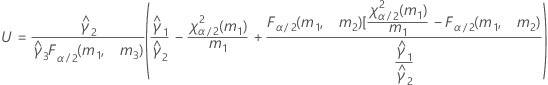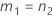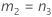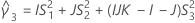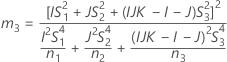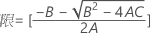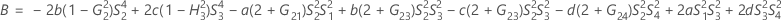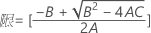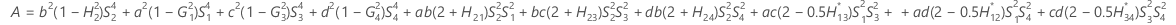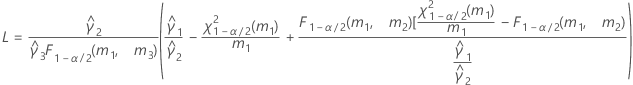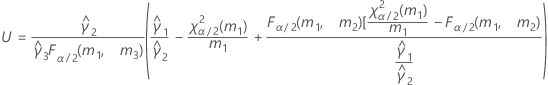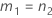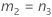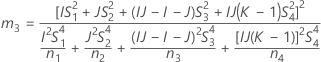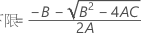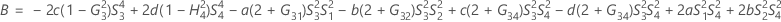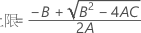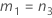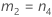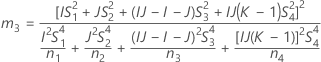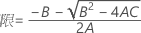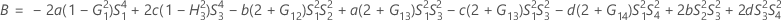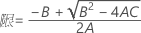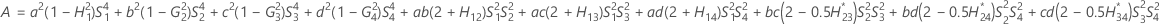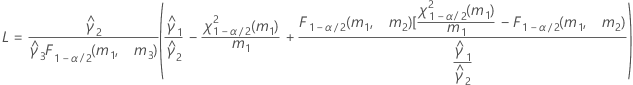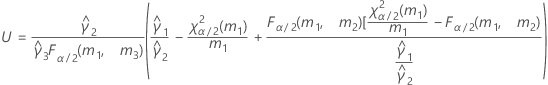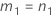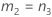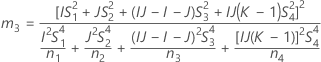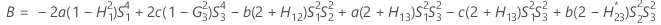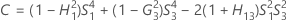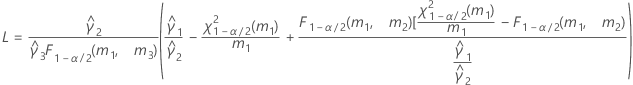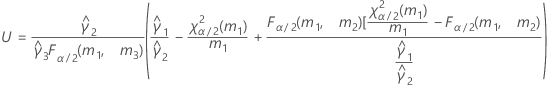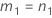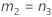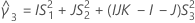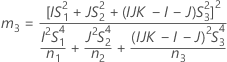このトピックの内容
繰り返し性の分散と合計分散の比の信頼区間
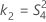
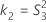
測定者を含む場合
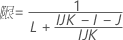
測定者と交互作用項が含まれている場合、使用できる計算方法は2つあります。Minitabでは最初に、改良大標本法(MLS)を使用して限界を計算します。計算中に特定の条件が満たされなかった場合には、Satterthwaiteの近似が使用されます。片側信頼限界を計算するには、HおよびGでα/2をαに置き換えます。
- MLS法
-
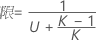
- Satterthwaiteの近似
- 上限と下限の計算式は、LおよびUが次のように定義される以外は、そのままです。
測定者項がない場合

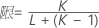
交互作用項がない場合
測定者と交互作用項が含まれている場合、使用できる計算方法は2つあります。Minitabでは最初に、改良大標本法(MLS)を使用して限界を計算します。計算中に特定の条件が満たされなかった場合には、Satterthwaiteの近似が使用されます。片側信頼限界を計算するには、HおよびGでα/2をαに置き換えます。
- MLS法
-
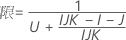
- Satterthwaiteの近似
- 上限と下限の計算式は、LおよびUが次のように定義される以外は、そのままです。
表記
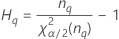
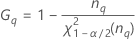
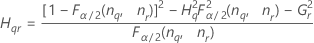
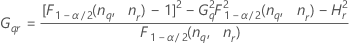
| 用語 | 説明 |
|---|---|
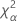 | 自由度がnqのカイ二乗分布の第α*100百分位数 |
| J | 測定者数 |
| I | 部品数 |
| K | 反復数 |
再現性の分散と合計分散の比の信頼区間
交互作用項がある場合
使用できる計算方法は2つあります。Minitabでは最初に、改良大標本法(MLS)を使用して限界を計算します。計算中に特定の条件が満たされなかった場合には、代替の近似が使用されます。片側信頼限界を計算するには、HおよびGでα/2をαに置き換えます。
- MLS法
- 2次方程式を解くことによって、近似の(1 – α)*100%信頼区間の下限と上限が計算されます。
- 2番目の方法
- 近似の(1 – α)*100%信頼区間の下限と上限は、次のように計算されます。
交互作用項がない場合
使用できる計算方法は2つあります。Minitabでは最初に、改良大標本法(MLS)を使用して限界を計算します。計算中に特定の条件が満たされなかった場合には、代替の近似が使用されます。片側信頼限界を計算するには、HおよびGでα/2をαに置き換えます。
- MLS法
- 2次方程式を解くことによって、近似の(1 – α)*100%信頼区間の下限と上限が計算されます。下限Lは、次の方程式の小さい方の解をJ倍したものです。
- 2番目の方法
- 近似の(1 – α)*100%信頼区間の下限と上限は、次のように計算されます。
表記
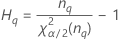
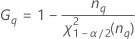
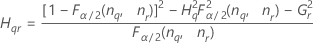
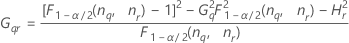
| 用語 | 説明 |
|---|---|
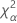 | 自由度がnqのカイ二乗分布の第α*100百分位数 |
| J | 測定者数 |
| I | 部品数 |
| K | 反復数 |
| a | I |
| b | J |
| c | (IJ – I –J) |
| d | IJ(K-1) |
| e | I – 1 |
測定者の分散と合計分散の比の信頼区間
使用できる計算方法は2つあります。Minitabでは最初に、改良大標本法(MLS)を使用して限界を計算します。計算中に特定の条件が満たされなかった場合には、代替の近似が使用されます。片側信頼限界を計算するには、HおよびGでα/2をαに置き換えます。
- MLS法
- 2次方程式を解くことによって、近似の(1 – α)*100%信頼区間の下限と上限が計算されます。
- 2番目の方法
- 近似の(1 – α)*100%信頼区間の下限と上限は、次のように計算されます。
表記
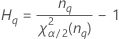
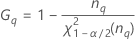
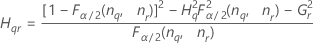
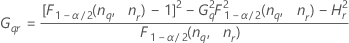
| 用語 | 説明 |
|---|---|
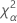 | 自由度がnqのカイ二乗分布の第α*100百分位数 |
| J | 測定者数 |
| I | 部品数 |
| K | 反復数 |
交互作用分散と全分散の比の信頼区間
使用できる計算方法は2つあります。Minitabでは最初に、改良大標本法(MLS)を使用して限界を計算します。計算中に特定の条件が満たされなかった場合には、代替の近似が使用されます。片側信頼限界を計算するには、HおよびGでα/2をαに置き換えます。
- MLS法
- 2次方程式を解くことによって、近似の(1 – α)*100%信頼区間の下限と上限が計算されます。
- 2番目の方法
- 近似の(1 – α)*100%信頼区間の下限と上限は、次のように計算されます。
表記
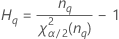
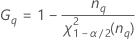
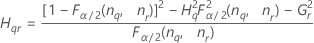
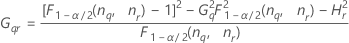
| 用語 | 説明 |
|---|---|
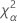 | 自由度がnqのカイ二乗分布の第α*100百分位数 |
| J | 測定者数 |
| I | 部品数 |
| K | 反復数 |
部品の分散と合計分散の比の信頼区間
測定者項と交互作用項がある場合
使用できる計算方法は2つあります。Minitabでは最初に、改良大標本法(MLS)を使用して限界を計算します。計算中に特定の条件が満たされなかった場合には、代替の近似が使用されます。片側信頼限界を計算するには、HおよびGでα/2をαに置き換えます。
- MLS法
- 2次方程式を解くことによって、近似の(1 – α)*100%信頼区間の下限と上限が計算されます。
- 2番目の方法
- 近似の(1 – α)*100%信頼区間の下限と上限は、次のように計算されます。
測定者項がない場合
下限 = 1 - (繰り返し性の分散と合計分散の比の下限)
上限 = 1 - (繰り返し性の分散と合計分散の比の上限)
交互作用項がない場合
- MLS法
- 2次方程式を解くことによって、近似の(1 – α)*100%信頼区間の下限と上限が計算されます。
- 2番目の方法
- 近似の(1 – α)*100%信頼区間の下限と上限は、次のように計算されます。
表記
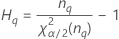
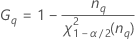
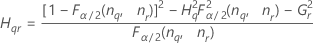

| 用語 | 説明 |
|---|---|
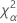 | 自由度がnqのカイ二乗分布の第α*100百分位数 |
| J | 測定者数 |
| I | 部品数 |
| K | 反復数 |
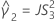
ゲージの分散と合計分散の比の信頼区間
下限 = 1 - (部品の分散と合計分散の比の信頼区間の下限)
上限 = 1 - (部品の分散と合計分散の比の信頼区間の上限)