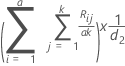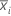分散分析法の分散成分
各要因による分散成分。
相互作用項を使うと
分散分析モデルに測定者*部品交互作用が含まれている場合、分散成分は次のように計算されます。
- 繰り返し性
-
繰り返し性 = MS繰り返し性
- 測定者
-

- 測定者*部品
-

- 部品間
-

- 再現性
- 再現性 = 分散成分測定者 +分散成分測定者*部品
- 合計ゲージR&R
- 合計ゲージR&R = 分散成分繰り返し性 + 分散成分再現性
- 全変動
- 全変動 = 分散成分合計ゲージR&R + 分散成分部品間
交互作用項なし
分散分析モデルに測定者*部品交互作用が含まれていない場合、分散成分は次のように計算されます。
- 繰り返し性
-
繰り返し性 = MS繰り返し性
- 測定者
-

- 部品間
-
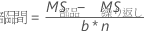
- 再現性
- 再現性 = 分散成分測定者
- 合計ゲージR&R
- 合計ゲージR&R = 分散成分繰り返し性 + 分散成分再現性
- 全変動
- 全変動 = 分散成分合計ゲージR&R + 分散成分部品間
分散成分が負の場合、ゲージR&Rでは0と表示されます。
Xbar-R法の分散
各要因による分散。
- 繰り返し性
- 機器による変動、標準偏差は次のように計算します。
- 再現性
-
測定者による変動、標準偏差は次のように計算します。
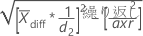
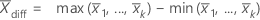
- 部品間
-
標準偏差は次のように計算します。
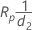
- 合計ゲージR&R
-
標準偏差は次のように計算します。

- 全変動
-
標準偏差は次のように計算します。

寄与度
%寄与度は各分散成分と分散全体の割合です。%寄与度は、全変動によって分割されたソースごとの分散成分として計算され、100を掛けて百分率として表現します。寄与度は、各分散成分を全変動で割り、100を掛けたものです。この列のパーセントの合計は100になります。

標準偏差
標準偏差(SD)は、変動のソースごとの標準偏差です。標準偏差は、そのソースの分散成分の平方根と等しくなります。
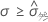 この場合、標準偏差の合計はσであり、次のようになります。
この場合、標準偏差の合計はσであり、次のようになります。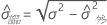 。
。- 他方、Minitabではデータを使用して標準偏差と以下を推定します。
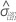 。
。
| 用語 | 説明 |
|---|---|
 | 過去の標準偏差 |
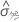 | データから計算されたゲージの標準偏差の合計 |
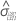 | 部品間の標準偏差 |
基準変動
基準変動は、6または基準変動で指定した乗数を掛けた変動のソースごとの標準偏差として計算します。
通常、工程変動は6sとして定義されます。ここでsは、母集団の標準偏差(σまたはシグマと表されます)の推定値としての標準偏差です。データが正規分布の場合、約99.73%のデータが平均から標準偏差の6倍以内の範囲にあります。異なる割合のデータを定義するには、標準偏差に別の乗数を使用します。たとえば、99%のデータの範囲を知るには、乗数にデフォルトの6ではなく5.15を使用します。
%基準変動と信頼区間
%基準変動は、全変動で割って100を掛けた変動のソースごとの基準変動として計算します。
%基準変動は、その要因の計算された分散成分の平方根です。したがって、分散成分の寄与度の合計は100になりますが、%基準変動の合計は100になりません。

信頼区間
L と寄与パーセントの下限と上限である場合、スタディ変動の対応するパーセントの信頼区間は次のようになります:
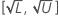
%公差と信頼区間
%公差とは、各成分の公差のパーセントです。
公差(上側規格限界 - 下側規格限界)が指定されると、各成分の基準変動を指定された公差で割ることによって%公差が計算されます。

片方の規格限界のみが指定された場合、%公差は、各成分の基準変動を片側公差で割ったものの半分です。片側公差は、指定された規格限界を全測定値の平均から引いたものの絶対値です。
Minitabでは、[オプション]サブダイアログボックスで、工程公差(上側規格限界 - 下側規格限界)または規格限界を入力した場合のみ、この値が表示されます。
信頼区間
LおよびUを分散成分の下限と上限とすると、対応する%公差の信頼区間は次のようになります。

| 用語 | 説明 |
|---|---|
| k | kは分析定数で、デフォルト値は6です |
%工程変動と信頼区間
%工程変動は工程変動のパーセントで、標準偏差の経験値に対する推定標準偏差の比として計算されます。

この値は、標準偏差の経験値を[オプション]サブダイアログボックスに入力した場合のみ表示されます。
信頼区間
LおよびUを分散成分の下限と上限とすると、対応する工程変動の信頼区間は次のようになります。

| 用語 | 説明 |
|---|---|
| k | kは分析定数で、デフォルト値は6です |