あるエンジニアが予想される工程変動範囲を代表する10個の部品を選択します。3名の測定者がその10個の部品をランダムな順序で3回ずつ測定します。
エンジニアが交差ゲージR&R分析を実行し、測定システムが原因で発生している可能性のある測定値の変動を評価します。
- 標本データを開く、 ゲージデータ.MWX.
- を選択します。
- 部品番号に部品を入力します。
- 測定者に測定者を入力します。
- 測定データに測定値を入力します。
- 分析法で、分散分析を選択します。
- オプションボタンをクリックします。工程公差で、上方-下方規格限界を選択して、8と入力します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
こちらの二元配置分散分析表は、部品、測定者、部品と測定者の交互作用の各項を含みます。交互作用のp値が0.05以上の場合は有意ではないため、Minitabではその交互作用が完全モデルから除外されます。この例では、p値は0.974であるため、最終モデルから交互作用を除外した2番目の二元配置分散分析表が生成されます。
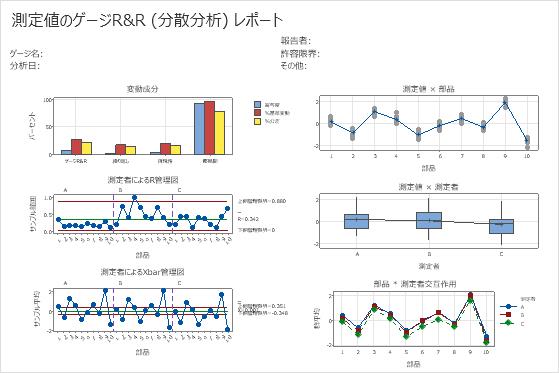
測定誤差の各要因からの変動を全変動と比較して評価するには分散成分(VarComp)を使用します。これらの結果では、ゲージR&R表の寄与度の列に、部品間の変動が92.24%であると表示されています。この値は、合計ゲージR&Rの7.76%よりはるかに大きいです。したがって、変動の大部分が、部品間の差によることがわかります。
測定システムの変動を全変動と比較する際には、%基準変動を使用します。合計ゲージR&Rは基準変動の27.86%です。合計ゲージR&R寄与度は用途によっては許容できる場合があります。詳細は、測定システムは許容範囲内かを参照してください。
このデータでは知覚区分数が4です。AIAGの基準では、値が5以上のときに適切な測定システムとみなされます。詳細は、ゲージR&R分析における異なるカテゴリの数の使用を参照してください。
グラフから、測定システムに関する次の情報も得られます。
- 変動成分グラフでは、部品間の寄与度が合計ゲージR&Rよりも大きくなっています。したがって、変動の大部分が、部品間の差によることがわかります。
- 作業者によるR管理図を見ると、測定者Bによる部品の測定値は一貫していないことがわかります。
- 測定者別Xbar管理図では、ほとんどの点が管理限界を超えています。したがって、変動の大部分が、部品間の差によることがわかります。
- 部品別グラフは、部品間の差が大きいことを示しています。
- 測定者別グラフでは、測定者間の差は部品間の差より小さくなっていますが有意です(p値 = 0.00)。測定者Cの測定値は、他の測定者よりやや低くなっています。
- 測定者*部品交互作用グラフでは、直線はほぼ平行で、表に表示されている測定者*部品交互作用のp値は0.974です。これらの結果は各部品と測定者の間に有意な交互作用が存在しないことを示しています。
二元配置の分散分析表 (交互作用あり)
| 要因 | 自由度 | 平方和 | 平均平方 | F値 | p値 |
|---|---|---|---|---|---|
| 部品 | 9 | 88.3619 | 9.81799 | 492.291 | 0.000 |
| 測定者 | 2 | 3.1673 | 1.58363 | 79.406 | 0.000 |
| 部品 * 測定者 | 18 | 0.3590 | 0.01994 | 0.434 | 0.974 |
| 繰り返し性 | 60 | 2.7589 | 0.04598 | ||
| 合計 | 89 | 94.6471 |
二元配置の分散分析表 (交互作用なし)
| 要因 | 自由度 | 平方和 | 平均平方 | F値 | p値 |
|---|---|---|---|---|---|
| 部品 | 9 | 88.3619 | 9.81799 | 245.614 | 0.000 |
| 測定者 | 2 | 3.1673 | 1.58363 | 39.617 | 0.000 |
| 繰り返し性 | 78 | 3.1179 | 0.03997 | ||
| 合計 | 89 | 94.6471 |
分散成分
| 要因 | 分散成分 | (分散成分の)寄与度 |
|---|---|---|
| 合計ゲージR&R | 0.09143 | 7.76 |
| 繰り返し性 | 0.03997 | 3.39 |
| 再現性 | 0.05146 | 4.37 |
| 測定者 | 0.05146 | 4.37 |
| 部品間 | 1.08645 | 92.24 |
| 全変動 | 1.17788 | 100.00 |
工程公差 = 8
ゲージ評価
| 要因 | 標準偏差 (SD) | 基準変動 (6×SD) | %基準変動(%SV) | %公差 (SV/公差) |
|---|---|---|---|---|
| 合計ゲージR&R | 0.30237 | 1.81423 | 27.86 | 22.68 |
| 繰り返し性 | 0.19993 | 1.19960 | 18.42 | 14.99 |
| 再現性 | 0.22684 | 1.36103 | 20.90 | 17.01 |
| 測定者 | 0.22684 | 1.36103 | 20.90 | 17.01 |
| 部品間 | 1.04233 | 6.25396 | 96.04 | 78.17 |
| 全変動 | 1.08530 | 6.51180 | 100.00 | 81.40 |
識別区分数 = 4