偏り
偏りは、測定システムの正確性の測度です。偏りは、参照部品の既知の標準値と観測された平均測定値の差として計算されます。
解釈
- 正の偏りはゲージの測度が高いことを示しています。
- 負の偏りはゲージの測度が低いことを示しています。
ゲージの測定が正確な場合、偏り度が小さくなります。偏りが統計的に有意かどうかを判断するにはp値を使用します。
繰り返し性と調整前の繰り返し性
繰り返し性は、測定システムの変動がどの程度ゲージに起因するかを表します。計数ゲージ分析では、参照値における許容確率を回帰推定し、繰り返し性を推定します。
調整前の繰り返し性とは、過大評価について調整する前に算出された繰り返し性です。Minitabでは、繰り返し性の推定値を調整因子1.08で割り、調整された繰り返し性を算出します。調整因子の1.08は、Automotive Industry Action Group (AIAG)の1から得られたものです。
解釈
繰り返し性の値が低い場合、ゲージが一貫した測定を行っていることを示しています。繰り返し性の値が高い場合、ランダムな変動を示しているか、または不適切な部品の選択やゲージの不良などの問題を示しています。
Minitabでは、調整された繰り返し性の値を計算に使用して、偏り = 0の帰無仮説を検定します。
正規確率プロット
正規確率プロットには参照値ごとの合格の割合が表示されます。偏りと繰り返し性の推定に使用できるゲージからの実際の測定値がないので、計算された合格の確率とすべての部品の既知の参照値を使用して正規分布曲線を適合することにより偏りと繰り返し性を計算します。
測定値エラーが正規分布に従う場合、計算された確率は直線に分布します。回帰線は確率に適合されます。
解釈
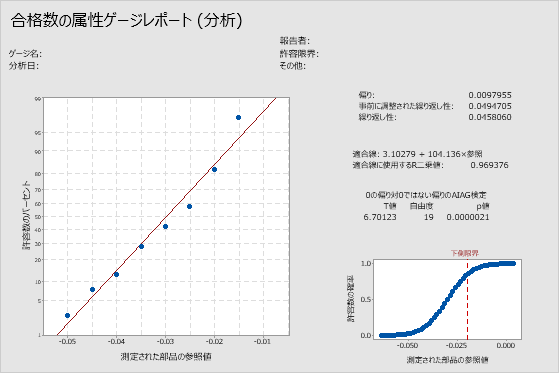
適合線
各部品の合格確率が計算されて、正規確率プロット上にプロットされます。正規確率プロット上では、プロットされた点のy値 = Φ–1(合格率)です。ここで、Φ–1は、標準正規累積分布関数の逆関数です。
適合回帰直線はプロットされた点を通って描かれます。
解釈
プロットされた点に適合線が良好に適合している場合、切片と傾きの値を使用して偏りと繰り返し性の値が計算されます。

このグラフは、適合線がデータに良好に適合していることを示しています。
適合線のR二乗
適合回帰線のR二乗(R2)の値は、回帰モデルで説明される合格応答の確率の分散の割合を示しています。
解釈
R2の範囲は0~100%です。通常、R2の値が高くなるほど、モデルのデータ適合度も高まります。90%より大きいR2の値は、データが非常に良好に適合していることを示しています。

この例では、R二乗は0.969376です。適合線は非常に良好にデータに適合し、モデルは分散の約97%を占めます。
T
Tは、偏り ≠ 0という対立仮説のt統計量です。
t検定では、この観測されたt統計量を自由度が(n-1)のt分布の棄却値と比較し、測定システムの偏りが統計的に優位であるかどうかを特定します。
自由度
自由度の値はp値の決定に使用されます。AIAG法の場合、自由度 = 試行数 - 1です。回帰法の場合、自由度 = 適合線を作成するために使用する点の数 - 2です。
p値
測定システムの偏りが統計的に有意かどうかを決定するには、p値と有意水準を比較します。通常、0.05の有意水準(αまたはアルファと呼ばれる)は適切です。0.05の有意水準は、有意な偏りがないときに偏りが存在すると結論付ける確率が5%あることを示しています。
解釈
p値が小さいほど、帰無仮説を棄却するための強力な証拠となります。p値がα値未満の場合は、測定システムの偏りが0に等しいという帰無仮説を棄却することができます。
ゲージの性能曲線
ゲージの性能曲線には、推定された合格の確率が項目の参照値の関数として表示されます。垂直参照線は、分析に入力した限界を示しています。
解釈
下側公差限界を指定すると、参照値と許容確率は増加する傾向を示します。上方許容限界を指定すると、参照値が増加するにつれて許容確率は減少します。
ゲージに上側限界と下側限界があり、誤差の線形性と一様性を仮定できる場合、ゲージの性能曲線上に上側公差限界と下側公差限界の両方を表示できます。曲線は左右対称に見えます。
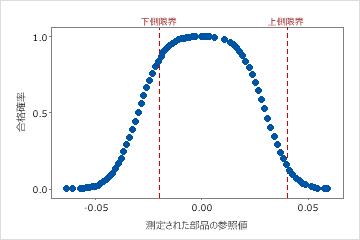
このデータの場合、項目の下側公差限界である-0.020での合格確率は高くなっています。参照値が0.01になるまでは参照値が増加するにつれて合格確率が増加します。その後、合格確率は減少します。上側公差限界(H限界)での合格確率は約0.15です。
