このトピックの内容
Cohenのκ統計量(未知の標準)
- 検査者内 — 検査者が行った試行がちょうど2回である
- 検査者間 — ちょうど2人の検査者がそれぞれ1回のみの試行を行った
特定の応答値に対して、1つのカテゴリ内でその値に等しくない応答をすべてまとめることによってκを計算できます。その後、2X2表を使用してκを計算できます。
計算式
真の標準が未知の場合、Minitabでは次のようにしてCohenのκを推定します。
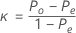
| 試行B(または検査者B) | |||||
| 試行A(または検査者A) | 1 | 2 | ... | k | 合計 |
| 1 | p11 | p12 | ... | p1k | p1+ |
| 2 | p21 | p22 | ... | p2k | P2+ |
| .... | |||||
| k | pk1 | pk2 | ... | pkk | pk+. |
| 合計 | p.+1 | p.+2 | ... | p.+k | 1 |
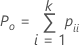
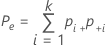
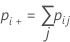
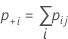

表記
| 用語 | 説明 |
|---|---|
| Po | 観測された一致率 |
| pii | 二元表の対角線上の各値 |
| Pe | k人の検査者が一致する回数の期待される比率 |
| nij | i行目、j列目のサンプル数 |
| N | サンプル総数 |
Cohenのκ統計量(既知の標準)
分類が名義値の場合はCohenのκ統計量を使用します。標準が既知で、Cohenのκを求めることを選択した場合、Minitabでは、下記の計算式を使用してκ統計量が計算されます。
既知の標準を持つ試行の一致性に対するκ係数は、これらのκ係数の平均です。
計算式
真の標準が既知の場合、最初に各試行からのデータと既知の標準を使用してκを計算します。
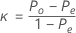
| 標準 | |||||
| 試行A | 1 | 2 | ... | k | 合計 |
| 1 | p11 | p12 | ... | p1k | p1+ |
| 2 | p21 | p22 | ... | p2k | P2+ |
| .... | |||||
| k | pk1 | pk2 | ... | pkk | pk+. |
| 合計 | p.+1 | p.+2 | ... | p.+k | 1 |
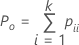
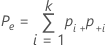
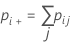
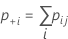

表記
| 用語 | 説明 |
|---|---|
| Po | 観測された一致率 |
| pii | 二元表の対角線上の各値 |
| Pe | k人の検査者が一致する回数の期待される比率 |
| nij | i行目、j列目のサンプル数 |
| N | サンプル総数 |
Cohenのκの有意性検定
評価が独立している(κ = 0)という帰無仮説を検定するには、次の式を使用します。
z = κ / κの標準誤差
これは片側検定です。帰無仮説の下では、zは標準正規分布に従います。zが棄却値αより有意に大きい場合は帰無仮説を棄却します。
計算式
各試行および標準に対するκの標準誤差は、次のようになります。
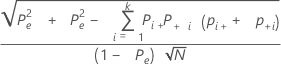
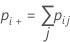
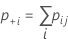
表記
| 用語 | 説明 |
|---|---|
| Pe | k人の検査者が一致する回数の期待される比率 |
| N | サンプル総数 |
Fleissのκ統計量(未知の標準)
- ケース1—各検査者内の一致
- 各検査者内の一致を表すκ係数を計算します。
- ケース2—すべての検査者間の一致
- すべての検査者間の一致を表すκ係数を計算します。
全体のκの計算式
xijはカテゴリjに分類されたサンプルiの評価数です。ここでiは1~n、jは1~kです。
全体のκ係数は次のように定義されます。
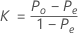
ここで、
Poは、m回の試行内で観測された対の一致率です。
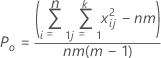
Peは、評価が試行ごとに独立している場合に予想される一致率です。
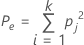
pjは、カテゴリjの全体の評価率を表します。
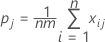
PoとPeをKに代入すると、全体のκ係数は次の式で推定されます。
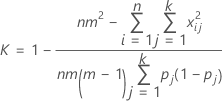
| 用語 | 説明 |
|---|---|
| k | カテゴリの合計数 |
| m | 試行数—ケース1の場合は各検査者の試行数、ケース2の場合は全検査者の試行数。 |
| n | サンプル数 |
| xij | カテゴリjに分類されたサンプルiの評価数 |
単一カテゴリのκの計算式
k個のカテゴリのうちの1つの分類(たとえばj番目)に関する一致を測定するには、目的のカテゴリ以外のすべてのカテゴリを1つにまとめて、上記の式を適用できます。その結果として得られるj番目のカテゴリのκ統計量の計算式は次のようになります。
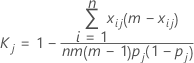
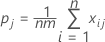
ここで、
| 用語 | 説明 |
|---|---|
| k | カテゴリの合計数 |
| m | 試行数—ケース1の場合は各検査者の試行数、ケース2の場合は全検査者の試行数。 |
| n | サンプル数 |
| xij | カテゴリjに分類されたサンプルiの評価数 |
Fleissのκの有意性検定(未知の標準)
帰無仮説H0はκ = 0です。対立仮説H1はκ > 0です。
帰無仮説の下では、Zはおおよそ正規分布に従い、p値を計算するために使用されます。
計算式
κ > 0かどうかを検定するには、次のZ統計量を使用します。

Var (K)は次のように計算されます。
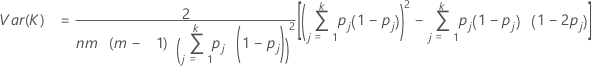
j番目のカテゴリに対してκ > 0かどうかを検定するには、次のZ統計量を使用します。

Var (Kj)は次のように計算されます。

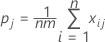
表記
| 用語 | 説明 |
|---|---|
| K | 全体のκ統計量 |
| Kj | j番目のカテゴリのκ統計量 |
| k | カテゴリの合計数 |
| m | 試行数—ケース1の場合は各検査者の試行数、ケース2の場合は全検査者の試行数。 |
| n | サンプル数 |
| xij | カテゴリjに分類されたサンプルiの評価数 |
Fleissのκ統計量(既知の標準)
各サンプルの標準評価が既知の場合は、次の手順を使用して全体のκおよび特定のカテゴリのκを計算します。
m回の試行を行ったと仮定します。
注
Fleissのκ統計量(未知の標準)の計算式を参照してください。
- 各試行に対して、試行の評価と標準の評価を使用してκを計算します。 つまり、標準を別の試行として扱い、標準が未知の場合の2回の試行に対するκの計算式を使用してκを推定します。
- m回すべての試行に対して計算を繰り返します。これで、全体のκ値がm個と特定カテゴリ値に対するκ値がm個得られます。
標準が既知の場合の全体のκは、m個すべての全体のκ値の平均です。
同様に、標準が既知の場合の特定カテゴリのκは、特定のカテゴリ値に対するm個すべてのκの平均です。
Fleissのκの有意性検定(既知の標準)
帰無仮説H0はκ = 0です。対立仮説H1はκ > 0です。
帰無仮説の下では、Zはおおよそ正規分布に従い、p値を計算するために使用されます。

ここで、Kはκ統計量で、Var(K)はκ統計量の分散です。
注
Fleissのκ統計量(未知の標準)の計算式を参照してください
m回の試行を行ったと仮定します。
- 各試行に対して、試行の評価と標準の評価を使用してκの分散を計算します。 つまり、標準を2回目の試行として扱い、標準が未知の場合の2回の試行に対するκの分散の計算式を使用して分散を計算します。
- m回すべての試行に対して計算を繰り返します。これで、全体のκの分散がm個と特定カテゴリに対するκの分散がm個得られます。
標準が既知の場合の全体のκの分散は、全体のκのm個の分散の和をm2で割ったものになります。
同様に、標準が既知の場合の特定カテゴリのκの分散は、特定のカテゴリに対するm個κの分散の和をm2で割ったものになります。
