属性の一致性分析の例

ある布プリント会社の布検査者は綿織物のプリント品質を1～5段階で評価します。品質エンジニアは、検査者の評価の一貫性と正確性を評価したいと考えています。エンジニアは、4人の検査者に30枚の布地サンプルのプリント品質を2回、ランダムな順序で評価するよう依頼します。

このデータには各サンプルの既知の標準が含まれるため、品質エンジニアは評価の一貫性と正確性を他の検査者と比較すると共にこの標準と比較することもできます。

標本データを開く、布プリント品質.MWX.
統計 > 品質ツール > 属性の一致性分析。
データの配列で、属性列を選択し、応答を入力します。
サンプルにサンプルを入力します。
検査者に検査者を入力します。
既知の標準・属性に標準を入力します。
属性データは順序カテゴリ(C)を選択します。
OKをクリックします。

結果を解釈する

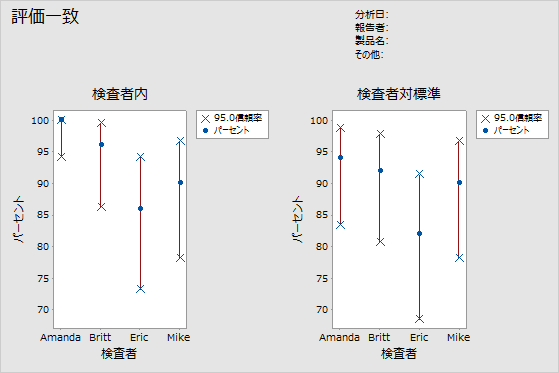
検査者内表: 各検査者は各サンプルを2回以上評価するため、エンジニアは各検査者の一貫性を評価できます。; 検査者の一致率は、Amandaの100%からEricの86%まで、すべて良好です。; すべての検査者およびすべての応答に対して、α = 0.05でFleissのκ統計量のp値は0.0000です。したがって、一致は偶然の所産であるという帰無仮説を棄却できます。; この例では順序評価が用いられているため、エンジニアはKendallの一致係数を調べます。すべての検査者のKendallの一致係数は、0.98446から1.000の範囲にあり、一致度が高いことを示しています。
各検査者対標準表: 各サンプルには既知の標準があるため、エンジニアは各検査者の評価の正確性と一貫性を評価できます。; 各検査者が50個の布地サンプルを評価しました（検査数）。Amandaは試行全体で47サンプルについて正しく評価しました（一致数）。一致比率は94%です。Ericは試行全体で41サンプルについて正しく評価しました。一致比率は82%です。; すべての検査者およびすべての応答に対して、α = 0.05でFleissのκのp値は0.0000です。したがって、一致は偶然の所産であるという帰無仮説を棄却できます。; すべての検査者のKendallの相関係数は、0.951863から0.975168の範囲にあり、標準との一致度が高いことが確認できます。
検査者間表: 検査者間表は、サンプル50個中37個で検査者間の評価が一致していることを示しています。; 全体のκ値は0.881705で、検査者間の評価の絶対一致度が高いことを示しています。Kendallの一致係数は0.976681で、関連性が強いことを確認できます。; 検査者間統計量では、検査者の評価と標準との比較は行われません。検査者間で評価が一貫していても、これらの統計量は評価が正しいかどうかを示すものではありません。
すべての検査者対標準表: 各サンプルには既知の標準があるため、エンジニアはすべての検査者の評価の正確性を評価できます。; すべての検査者の評価は50個中37個が既知の標準と一致しており、一致比率は74.0%です。; 全体のκ値は0.912082で、検査者と標準の間で評価の絶対一致度が高いことを示しています。Kendallの一致係数は0.965563で、関連性が強いことを確認できます。; すべての検査者対標準の統計量では、検査者の評価と標準を比較します。エンジニアは、検査者の評価が一貫していて正確であると結論付けることができます。

注

出力のp値0.0000は四捨五入されています。ただし、p値は非常に低く、0.00005より小さい値であると問題なく結論付けることができます。

検査者	検査数	一致数	パーセント	95%信頼区間
Amanda	50	50	100.00	(94.18, 100.00)
Britt	50	48	96.00	(86.29, 99.51)
Eric	50	43	86.00	(73.26, 94.18)
Mike	50	45	90.00	(78.19, 96.67)

検査者	応答	κ	SE　Kappa	z値
Amanda	1	1.00000	0.141421	7.0711
	2	1.00000	0.141421	7.0711
	3	1.00000	0.141421	7.0711
	4	1.00000	0.141421	7.0711
	5	1.00000	0.141421	7.0711
	全体	1.00000	0.071052	14.0741
Britt	1	1.00000	0.141421	7.0711
	2	0.89605	0.141421	6.3360
	3	0.86450	0.141421	6.1129
	4	1.00000	0.141421	7.0711
	5	1.00000	0.141421	7.0711
	全体	0.94965	0.071401	13.3002
Eric	1	0.83060	0.141421	5.8733
	2	0.84000	0.141421	5.9397
	3	0.70238	0.141421	4.9666
	4	0.70238	0.141421	4.9666
	5	1.00000	0.141421	7.0711
	全体	0.82354	0.071591	11.5034
Mike	1	1.00000	0.141421	7.0711
	2	0.83060	0.141421	5.8733
	3	0.81917	0.141421	5.7924
	4	0.86450	0.141421	6.1129
	5	0.86450	0.141421	6.1129
	全体	0.87472	0.070945	12.3295

検査者	係数	カイ二乗	自由度	p値
Amanda	1.00000	98.0000	49	0.0000
Britt	0.99448	97.4587	49	0.0000
Eric	0.98446	96.4769	49	0.0001
Mike	0.98700	96.7256	49	0.0001

検査者	検査数	一致数	パーセント	95%信頼区間
Amanda	50	47	94.00	(83.45, 98.75)
Britt	50	46	92.00	(80.77, 97.78)
Eric	50	41	82.00	(68.56, 91.42)
Mike	50	45	90.00	(78.19, 96.67)

検査者	応答	κ	SE　Kappa	z値
Amanda	1	1.00000	0.100000	10.0000
	2	0.83060	0.100000	8.3060
	3	0.81917	0.100000	8.1917
	4	1.00000	0.100000	10.0000
	5	1.00000	0.100000	10.0000
	全体	0.92476	0.050257	18.4006
Britt	1	1.00000	0.100000	10.0000
	2	0.83838	0.100000	8.3838
	3	0.80725	0.100000	8.0725
	4	1.00000	0.100000	10.0000
	5	1.00000	0.100000	10.0000
	全体	0.92462	0.050396	18.3473
Eric	1	0.91159	0.100000	9.1159
	2	0.81035	0.100000	8.1035
	3	0.72619	0.100000	7.2619
	4	0.84919	0.100000	8.4919
	5	1.00000	0.100000	10.0000
	全体	0.86163	0.050500	17.0622
Mike	1	1.00000	0.100000	10.0000
	2	0.91694	0.100000	9.1694
	3	0.90736	0.100000	9.0736
	4	0.92913	0.100000	9.2913
	5	0.93502	0.100000	9.3502
	全体	0.93732	0.050211	18.6674

属性の一致性分析の例

結果を解釈する

注

評価一致

Fleissのκ統計

Kendallの一致係数

評価一致

Fleissのκ統計

Kendallの相関係数

評価一致

Fleissのκ統計

Kendallの一致係数

評価一致

Fleissのκ統計

Kendallの相関係数

検査者	係数	SE　Coef	z値
Amanda	0.967386	0.0690066	14.0128
Britt	0.967835	0.0690066	14.0193
Eric	0.951863	0.0690066	13.7879
Mike	0.975168	0.0690066	14.1256

応答	κ	SE　Kappa	z値
1	0.954392	0.0267261	35.7101
2	0.827694	0.0267261	30.9695
3	0.772541	0.0267261	28.9058
4	0.891127	0.0267261	33.3429
5	0.968148	0.0267261	36.2248
全体	0.881705	0.0134362	65.6218

応答	κ	SE　Kappa	z値
1	0.977897	0.0500000	19.5579
2	0.849068	0.0500000	16.9814
3	0.814992	0.0500000	16.2998
4	0.944580	0.0500000	18.8916
5	0.983756	0.0500000	19.6751
全体	0.912082	0.0251705	36.2362