工程標準偏差は、シグマまたはσとも呼ばれます。σの経験値を入力すると、その経験値が使用されます。値を入力しないと、次のいずれかの方法を使用して、データからσが推定されます。
Rbar方法
Minitabでは各サブグループの範囲、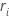
を使用して、を計算します。
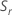、これはσの不偏推定値です。
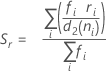
ここで
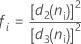
サブグループサイズが一定の場合、この式は次のように簡略化されます:
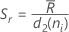
ここで、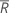
（Rbar）は、サブグループ範囲の平均で、次のように計算されます:
表記
| 用語 | 説明 |
|---|---|
| ri | サブグループiの範囲 |
| m | サブグループ数 |
| d2(·) | 括弧内に指定された値に対応する不偏化のための定数d2。 |
| ni | サブグループ内の観測値数 i |
| d3(·) | 括弧内に指定された値に対応する不偏化のための定数 d3。 |
併合標準偏差法
併合標準偏差（Sp）は、次の計算式で計算します。
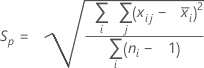
サブグループサイズが一定の場合、Spは次のように計算することもできます:
不偏化のための定数を使用する場合
併合標準偏差を使用してσを推定する場合、デフォルトで、不偏化のための定数、c4()が適用されます。
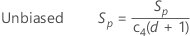
サブグループサイズが一定の場合、不偏Spは次のように計算することもできます:
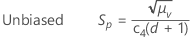
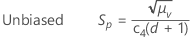
表記
| 用語 | 説明 |
|---|---|
| xij | i番目のサブグループのj番目の観測値 |
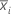 | サブグループiの平均 |
| ni | サブグループi内の観測値数 |
| μv | サブグループ分散の平均 |
| c4(·) | 括弧内に指定された値に対応する不偏化のための定数 c4。 |
| d | 次の計算式で求められる、Spの自由度:
 |
不偏化のための定数d2()、d3()、およびd4()
d2(N)は、標準偏差=1の正規母集団からのN個の観測値の範囲の期待値です。したがって、標準偏差=σの正規分布からのN個の観測値のサンプルの範囲をrとすると、E(r) = d2(N)σとなります。
d3(N)は、σ=1の正規母集団からのN個の観測値の範囲の標準偏差です。したがって、標準偏差=σの正規分布からのN個の観測値のサンプルの範囲をrとすると、stdev(r) = d3(N)σとなります。
与えられた値Nに対する不偏化のための定数を見つけるには、次の表を使用します。（Nの値を決定するには、目的の統計量の計算式を参照してください。）
Nの値が51～100の場合、d2(N)に次の近似値を使用します。
Nの値が26～100の場合、d3(N)およびd4(N)に次の近似値を使用します。
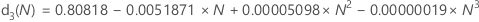
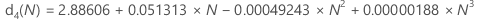
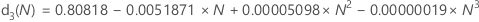
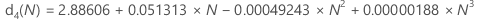
これらの定数の詳細については、次の文献を参照してください。
- D. J. Wheeler and D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
- H. Leon Harter (1960). "Tables of Range and Studentized Range". The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1.128 | 0.8525 | 0.954 |
| 3 | 1.693 | 0.8884 | 1.588 |
| 4 | 2.059 | 0.8798 | 1.978 |
| 5 | 2.326 | 0.8641 | 2.257 |
| 6 | 2.534 | 0.848 | 2.472 |
| 7 | 2.704 | 0.8332 | 2.645 |
| 8 | 2.847 | 0.8198 | 2.791 |
| 9 | 2.97 | 0.8078 | 2.915 |
| 10 | 3.078 | 0.7971 | 3.024 |
| 11 | 3.173 | 0.7873 | 3.121 |
| 12 | 3.258 | 0.7785 | 3.207 |
| 13 | 3.336 | 0.7704 | 3.285 |
| 14 | 3.407 | 0.763 | 3.356 |
| 15 | 3.472 | 0.7562 | 3.422 |
| 16 | 3.532 | 0.7499 | 3.482 |
| 17 | 3.588 | 0.7441 | 3.538 |
| 18 | 3.64 | 0.7386 | 3.591 |
| 19 | 3.689 | 0.7335 | 3.64 |
| 20 | 3.735 | 0.7287 | 3.686 |
| 21 | 3.778 | 0.7242 | 3.73 |
| 22 | 3.819 | 0.7199 | 3.771 |
| 23 | 3.858 | 0.7159 | 3.811 |
| 24 | 3.895 | 0.7121 | 3.847 |
| 25 | 3.931 | 0.7084 | 3.883 |
| N | d2(N) |
|---|---|
| 26 | 3.964 |
| 27 | 3.997 |
| 28 | 4.027 |
| 29 | 4.057 |
| 30 | 4.086 |
| 31 | 4.113 |
| 32 | 4.139 |
| 33 | 4.165 |
| 34 | 4.189 |
| 35 | 4.213 |
| 36 | 4.236 |
| 37 | 4.259 |
| 38 | 4.28 |
| 39 | 4.301 |
| 40 | 4.322 |
| 41 | 4.341 |
| 42 | 4.361 |
| 43 | 4.379 |
| 44 | 4.398 |
| 45 | 4.415 |
| 46 | 4.433 |
| 47 | 4.45 |
| 48 | 4.466 |
| 49 | 4.482 |
| 50 | 4.498 |
不偏化のための定数c4()およびc5()
c4()
c5()
表記
| 用語 | 説明 |
|---|---|
| Γ() | ガンマ関数 |
