シグマ（σ）は、工程の標準偏差です。σの経験値を入力すると、その経験値が使用されます。経験値を入力しない場合は、次のいずれかの方法を使用してデータからσが推定されます。
移動範囲平均法
移動範囲平均、
、長さwは、次の計算式で得られます。
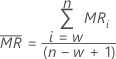
ここで、MRiは次のように計算される、観測値iの移動範囲です。
Minitabでは、
を使用して、σの偏りのない推定値であるSmrを計算します。
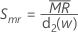
表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| w | 移動範囲の長さ。デフォルトは2です。 |
| d2() | 括弧内で指定された値に対応する、不偏化のための定数d2の値。 |
移動範囲中央値法
移動範囲中央値、
、の長さwは、次の計算式で得られます。
ここで、MRiは次のように計算される、観測値iの移動範囲です。
Minitabでは、
を使用して、σの偏りのない推定値であるSmrを計算します。
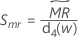
表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| w | 移動範囲の長さ。デフォルトは2です。 |
| d4() | 括弧内で指定された値に対応する、不偏化のための定数d4の値。 |
MSSDの平方根法
MSSDは、平方逐次的差分の平均（Mean of Squared Successive Differences）を表します。MSSDの平方根（SRMSSD）は、次のように計算されます。
不偏化のための定数を使用する場合
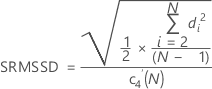
不偏化のための定数を使用しない場合
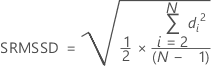
表記
| 用語 | 説明 |
|---|---|
| di | 観測値iの値と観測値i – 1の値の差 |
| N | 観測値数 |
| c4'(N) | 表からの不偏化のための定数 |
Rbar方法
Minitabでは各サブグループの範囲、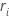
を使用して、を計算します。
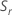、これはσの不偏推定値です。
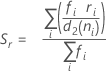
ここで
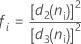
サブグループサイズが一定の場合、この式は次のように簡略化されます:
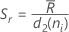
ここで、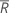
（Rbar）は、サブグループ範囲の平均で、次のように計算されます:
表記
| 用語 | 説明 |
|---|---|
| ri | サブグループiの範囲 |
| m | サブグループ数 |
| d2(·) | 括弧内に指定された値に対応する不偏化のための定数d2。 |
| ni | サブグループ内の観測値数 i |
| d3(·) | 括弧内に指定された値に対応する不偏化のための定数 d3。 |
Sbar法
不偏化のための定数を使用しない場合
不偏化のための定数を使用しない場合、Sbarはサブグループ標準偏差の平均です。
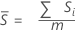
不偏化のための定数を使用する場合
不偏化のための定数、c4（ni）を使用する場合、Sbarは次のように計算します。
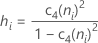
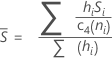
サブグループサイズが一定の場合、Sbarは次のように計算されます。
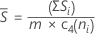
表記
| 用語 | 説明 |
|---|---|
| c4 (ni) | 括弧内に指定された値に対応する不偏化のための定数c4。 |
| Si | サブグループiの標準偏差 |
| m | サブグループ数 |
併合標準偏差法
併合標準偏差（Sp）は、次の計算式で計算します。
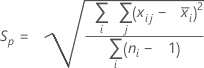
サブグループサイズが一定の場合、Spは次のように計算することもできます:
不偏化のための定数を使用する場合
併合標準偏差を使用してσを推定する場合、デフォルトで、不偏化のための定数、c4()が適用されます。
サブグループサイズが一定の場合、不偏Spは次のように計算することもできます:
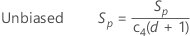
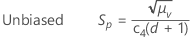
表記
| 用語 | 説明 |
|---|---|
| xij | i番目のサブグループのj番目の観測値 |
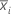 | サブグループiの平均 |
| ni | サブグループi内の観測値数 |
| μv | サブグループ分散の平均 |
| c4(·) | 括弧内に指定された値に対応する不偏化のための定数 c4。 |
| d | 次の計算式で求められる、Spの自由度:
 |
