プロットされた点
T二乗管理図にプロットされた点は、各サブグループのT2値です。一般化分散管理図にプロットされた点は、各サブグループの一般化分散統計量です。
解釈
工程が正常に管理されている場合、各点は上側管理限界より下にあり、工程は一般原因による変動のみを示します。上側管理限界より上にある点を調べます。多変量管理図の欠点の1つは、そのスケールがどの変数のスケールとも関連しておらず、管理外信号にその信号の原因となった変数(または変数の組み合わせ)が示されないという点です。
中心線
T二乗管理図の中心線は、T2統計量の理論的分布の中央値です。一般化分散管理図の中心線は、サンプル共分散行列の行列式です。
解釈
中心線を使用して、工程の性能と平均値の比較を観測します。工程が正常に管理されている場合、各点は中心線付近でランダムに変動します。
管理限界
管理限界は、中心線の上下に位置する水平方向のラインです。工程が管理外にあるかどうかを示し、サブグループ内で観測された変動、およびプロットされた点で期待される変動に基づいています。T二乗管理図には上側管理限界のみがあります。一般化分散管理図には上側管理限界と下側管理限界の両方があります。
分解されたT2値
分解されたT2値により、T2管理図上のすべての管理外データ点に対する各変数の寄与度が計算されます。
T2管理図の個々の点は、複数の変数を表す複合値です。このため、T2管理図には、結合された点の値に対する各変数の寄与度は表示されません。結合点の値は、管理外データ点の解釈を複雑にします。データ点がT2 管理図で管理外の場合、すべての変数、一部の変数または1つだけの変数が管理外状態に寄与したのかどうかを判断することはできません。しかし、分解されたT2値により、1つの変数が、他の変数よりも管理外状態に寄与したかどうかがわかります。
共分散行列
共分散行列は、複数の変数の分散と共分散を含む正方行列です。行列の対角エレメントには変数の分散値が配置され、対角から外れたエレメントには変数の可能なすべてのペア間の共分散値が配置されています。
分散共分散行列は、XとYの間の共分散値がYとXの間の共分散値と同じになるので、対称的な行列になります。したがって、変数のペアごとの共分散が行列内に2回現れることになり、i番目とj番目の変数の間の共分散が(i,j)と(j,i)の位置に表示されます。
共分散行列を保存した後、を選択して、共分散行列を表示します。
解釈
| X | Y | Z | |
| X | 2.0 | −0.86 | −0.15 |
| Y | −0.86 | 3.4 | 0.48 |
| Z | −0.15 | 0.48 | 0.82 |
変数は、対角線に沿って太字で表示されます。変数は、Xで2.0、Yで3.4、Zで0.82です。XとYの間の共分散は−0.86、XとZの間の共分散は−0.15、YとZの間の共分散は0.48です。
ステージ
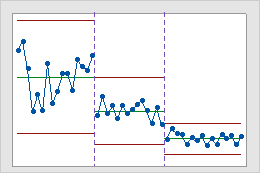
ステージを使用して、一定期間における工程の変化の様子を示す履歴データ管理図を作成します。Minitabでは、デフォルトでステージごとに中心線と管理限界を再計算します。詳細は、工程がどのように変化したのかを示すステージの追加を参照してください。
解釈
この履歴データ管理図には、新しい手順の実装前、実装中、および実装後を表す、工程の3つのステージが示されています。