Minitabで非正規工程能力分析を実行する場合、全体の工程能力インデックスは、デフォルトではZスコア法を使用して計算されます。
規格限界の変換
Zスコアを計算するために、最初に、分析のために指定した非正規分布に基づいて、規格限界外にある観測値の比率が特定されます。

このグラフの陰影領域は、分析のために指定された非正規分布を使用して、測定値Xが下側規格限界(LSL)より小さい確率であるP1を表します。この例では、指定された非正規分布はワイブルで、パラメータはデータから除外されており、P1 = 0.01です。

このグラフの陰影領域は、分析のために指定された非正規分布を使用して、測定値Xが上側規格限界(USL)より小さい確率であるP2を表します。この例では、指定された非正規分布はワイブルで、パラメータはデータから除外されており、P2 = 0.90です。
次に、確率P1およびP2を使用して、対応する標準正規分布のZ値が計算されます。このようにして、元の規格限界を、標準正規スケール上の対応するZ値で表すことができます。
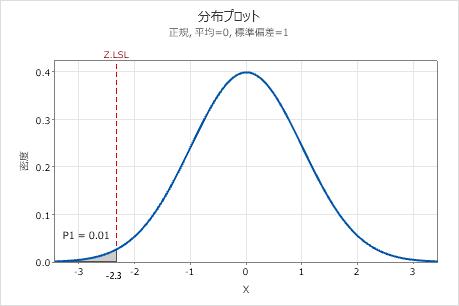
P1が標準正規分布上で表される場合、P1に対応するZ値はZ.LSLと呼ばれます。Z.LSLは、標準正規スケール内の下側規格限界です。この例では、Z.LSLは約−2.3です。

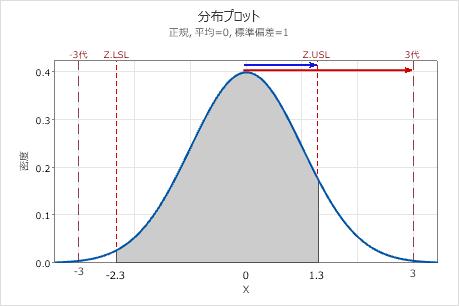
P2が標準正規分布上で表される場合、P2に対応するZ値はZ.USLと呼ばれます。Z.USLは、標準正規スケール内の上側規格限界です。この例では、Z.USLは約1.3です。
標準正規分布内での規格広がりを特定するには、Z.LSLの値をZ.USLの値から引きます。

この例では、規格広がりは、1.3 - (−2.3) = 3.6で、矢印によって示されています。
非正規工程能力インデックスの計算
次に、全体の工程能力インデックスが、標準正規規格広がりと標準正規分布の特定の広がりの関係に基づいて、計算されます。
Ppは、6-σ広がり(6)に対する標準正規規格広がりの比です。6-σ広がりには、標準正規分布からの工程測定値の99.74%が含まれます。

この例では、Ppは3.6/6 ≈ 0.6です。
PPLは、下側規格限界に対する片側規格広がり(Z.LSL)を6-σ広がりの半分(3)で割った比です。

この例では、PPLは−2.3/-3 ≈ 0.76です。
PPUは、上側規格限界に対する片側規格広がり(Z.USL)を6-σ広がりの半分(3)で割った比です。
この例では、PPUは1.3/3 ≈ 0.43です。
Ppkは、PPUとPPLの小さい方の値です。したがって、この例では、PpkはPPU ≈ 0.43です。
