標準偏差を推定
サブグループ間/サブグループ内工程能力分析は、次の4つの標準偏差に基づいています。
サブグループ内標準偏差
σwithinは、サブグループ内の変動(たとえば、1シフト、1人の作業者、または1つの材料バッチなど)の推定値です。Minitabでは、次のいずれかの方法を使用してσwithinを推定します。
- [併合標準偏差]:

ここで、
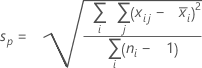
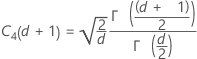
注
デフォルトの方法を変更し、不偏化のための定数を使用しない方法を選択すると、σwithinはSpによって推定されます。
用語 説明 d Sp= Σ (ni- 1)の場合の自由度 Xij i番目のサブグループのj番目の観測値 X̅i i番目のサブグループの平均 ni i番目のサブグループ内の観測値数 C4(d+1) 不偏化のための定数 Γ(·) ガンマ関数 - サブグループ範囲の平均(Rbar):

ここで、
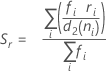
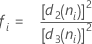
nがすべての同じ場合:
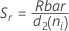
用語 説明 ri i番目のサブグループの範囲 d2 (ni) テーブルから読み出された不偏化のための定数(詳細は、不偏化のための定数d2()、d3()、d4()のセクションを参照してください) d3 (ni) テーブルから読み出された不偏化のための定数(詳細は、不偏化のための定数d2()、d3()、d4()のセクションを参照してください) ni i番目のサブグループ内の観測値数 - サブグループ標準偏差の平均(Sbar):

ここで、
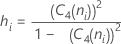
注
デフォルトの設定を変更し、不偏化のための定数を使用しない場合、σwithinはΣ Si / (サブグループ数)によって推定されます。
用語 説明 C4(ni) 不偏化のための定数(併合標準偏差で定義) Si サブグループiの標準偏差 ni i番目のサブグループ内の観測値数
サブグループ間標準偏差
σBetweenは、サブグループ間の変動(たとえば、一定の間隔、バッチ、または異なる作業者によって収集されたサブグループ)の推定値です。
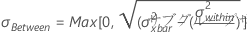
- 移動範囲の平均:
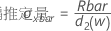
ここで、


用語 説明 Ri i番目の移動範囲 w 移動範囲で使用される観測値の数。デフォルトはw = 2です。 d2(w) テーブルから読み出された不偏化のための定数(詳細は、不偏化のための定数d2()、d3()、d4()のセクションを参照してください) - 移動範囲の中央値:
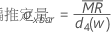
ここで、

用語 説明 MRi i番目の移動範囲 
MRiの中央値 w 移動範囲で使用される観測値の数。デフォルトはw = 2です。 d4(w) テーブルから読み出された不偏化のための定数(詳細は、不偏化のための定数d2()、d3()、d4()のセクションを参照してください) - 平均平方逐次的差分の平方根(MSSD):
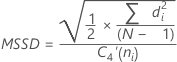
注
デフォルト設定を変更し、不偏化のための定数を使用しない場合、σwithinは次の式で推定されます。

用語 説明 di 逐次的グループ平均の差分 C4(ni) 不偏化のための定数(併合標準偏差で定義) C4'(ni) 不偏化のための定数 ≈ c4(ni)。ショウサイハ、不偏化のための定数c4'()のセクションを参照してください。 N 観測値の合計数 ni i番目のサブグループ内の観測値数
サブグループ間/内標準偏差

| 用語 | 説明 |
|---|---|
| σ2Between | サブグループ間の分散 |
| σ2within | サブグループ内の分散 |
全体の標準偏差

ここで、
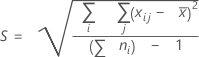
注
デフォルトでは、σoverallの推定の際、不偏化のための定数は使用されません。σoverallはSで推定されます。不編化のための定数を使用して全体の標準偏差を推定する場合、工程能力分析を行う際に推定サブダイアログボックスでこのオプションを変更することができます。常に不編化のための定数を使用するのをデフォルトにしたい場合は、を選択して、適切なオプションを選びます。
| 用語 | 説明 |
|---|---|
| Xij | i番目のサブグループのj番目の観測値 |
| X̅ | 工程平均 |
| ni | i番目のサブグループ内の観測値数 |
| C4 (N) | 不偏化のための定数(併合標準偏差で定義) |
| N(またはΣ ni) | 観測値の合計数 |
Box-Cox変換
Box-Cox変換は、次の表に示すように、変換によって標準化された変数の標準偏差を最小化するλ値を推定します。結果として得られる変換は、λ ҂ 0の場合はYλで、λ = 0の場合はln Yです。
Box-Cox法では、さまざまな種類の変換が探索されます。次の表は、いくつかの一般的な変換を示しています。ここで、Y'はデータYの変換です。
| λ値 | 変換 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
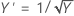 |
 |
 |
