U管理図
U管理図には、単位あたりの欠陥(不適合)数がプロットされます。中心線は、単位(またはサブグループ)あたりの欠陥数の平均値です。管理限界は、中心線から上下に標準偏差の3倍の距離の位置に設定され、サブグループ平均値の期待される変動量を示します。
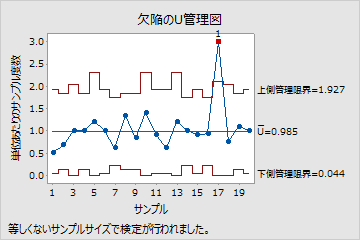
このU管理図は、ユニットあたりの欠陥率が、全サンプルで平均すると約1であることを示しています。1つの点が管理外にあるように見えます。
解釈
単位あたりの欠陥数を視覚的に監視したり、欠陥率が安定しており正常に管理されているかどうかを判断するには、U管理図を使用します。
赤の点は、サブグループが特殊原因についてのテストの1つ以上で不合格となり、正常に管理されていないことを示しています。管理外れの点がある場合は、工程が安定しておらず、工程能力分析の結果が信頼できないことを示します。管理外れの点の原因を特定し、特殊原因による変動を排除してから、工程能力を分析する必要があります。
特別原因についてのテスト
各管理図上のプロットされた点がランダムに管理限界内に分布しているかどうかを評価するには、特別原因についてのテストを行います。
解釈
調査が必要な観測値を特定し、データから特定のパターンおよびトレンドを識別するには、特別原因についてのテストを使用します。特別原因についてのテストはそれぞれ、データ内の特定のパターンやトレンドを検出し、工程の不安定性の異なる側面を明らかにします。
- [中心線から3σ以上離れた1点]
- テスト1では他のサブグループと比較したときに異常と判断されるサブグループが識別されます。このテストは管理外の状況の検出に必要であると広く認められています。工程内の小さなシフトが懸念される場合は、テスト2を補助的に使うとより感度の高い管理図を作成することができます。
- [連続する9点が中心線に対して同じ側にある]
- テスト2では、工程変動内のシフトが識別されます。工程内の小さなシフトが懸念される場合は、テスト2を補助的に使うとより感度の高い管理図を作成することができます。
- [連続する6点が増加、または減少している]
- テスト3では、トレンドが検出されます。このテストではその値が連続して増加または減少する長く連続する点が探されます。
- [連続する14点が交互に増減している]
- テスト4では系統的な変動が検出されます。プロセスにおける変動のパターンはランダムであることが理想ですが、テスト4で不合格となる点はその変動のパターンが予測可能であることを示している可能性があります。
累積DPUプロット
累積DPUプロット上の点は、各サンプルのDPU平均値を示します。点は、サンプルが収集された順序で表示されます。中央の水平線は、すべてのサンプルから計算されたDPU平均値を表します。上下の水平線は、DPU平均値の信頼区間の上限と下限を表します。
解釈
安定したDPU推定値を得るために十分なサンプルを収集したかどうかを判断するには、累積DPUプロットを使用します。
時間によって順序付けられたサンプルの単位あたりの欠陥数を調べて、収集するサンプルの増加に伴い推定値がどのように変化するかを調べます。いくつかのサンプルの後にDPUが安定するのが理想です。DPUが安定していることは、プロットされた点がDPU平均値の線に沿って平坦になることによって示されます。
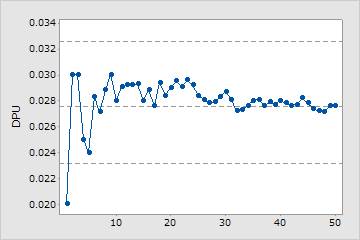
十分なサンプル
この工程能力分析にはユニットあたりの欠陥数の平均値を推定するのに十分なサンプルが使用されています。
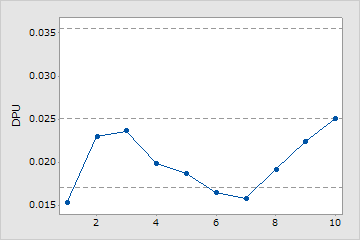
サンプル不足
この工程能力分析ではユニットあたりの欠陥数の平均値を推定するのに十分なサンプルが使用されていません。
ポアソンプロット
ポアソンプロットには、観測された欠陥数と期待される欠陥数が対比されて表示されます。対角線は、データがポアソン分布に完全に従っている場合に表示される場所を示しています。データがこの線から大きく外れている場合、ポアソン工程能力分析によって信頼できる結果が得られない可能性があります。
注
Minitabでは、サブグループサイズが等しい場合にポアソンプロットが表示されます。サブグループサイズが異なる場合は、欠陥率プロットが表示されます。詳細については、欠陥率プロットに関するセクションを参照してください。
解釈
データがポアソン分布に従っているかどうかを評価するには、ポアソンプロットを使用します。
プロットを調べ、プロットされた点がおおむね直線に沿っているかどうかを判断します。直線になっていなければ、データがポアソン分布からサンプル抽出されたという仮定は誤っている可能性があります。
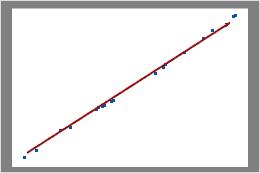
これらの結果では、データ点は線の付近に表示されています。データがポアソン分布に従っていると仮定できます。
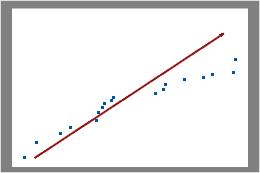
これらの結果では、データ点はプロットの右上部分で線の付近に表示されていません。これらのデータはポアソン分布に従っておらず、ポアソン工程能力分析を使用して信頼性の高い評価を行うことができません。
欠陥率プロット
欠陥率プロットには、各サブグループ内の単位あたりの欠陥数(DPU)と各サブグループのサイズが表示されます。中心線は、DPU平均値です。
注
サブグループサイズが異なる場合は、欠陥率プロットが表示されます。サブグループサイズが一定である場合は、ポアソンプロットが表示されます。詳細については、ポアソンプロットに関するセクションを参照してください。
解釈
単位あたりの欠陥数はサンプルサイズが異なっても一定であるという仮定を調べることにより、データがポアソンデータであることを確認するには、欠陥率プロットを使用します。
プロットを調べ、単位あたりの欠陥数(DPU)がサンプルサイズ全体にわたりランダムに分布しているか、あるいは何らかのパターンがあるかを評価します。データが中心線付近にランダムに表示される場合は、データがポアソン分布に従っていると判断します。
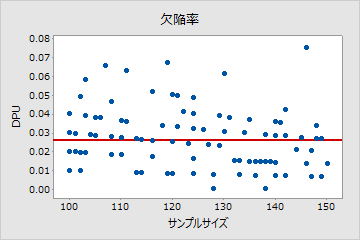
ポアソン
このプロットでは、点は中心線付近でランダムに散在しています。データがポアソン分布に従っていると仮定できます。
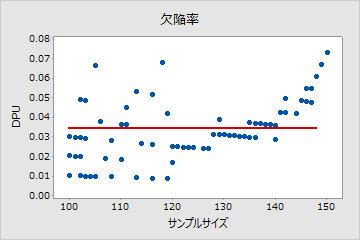
ポアソンでない
このプロットでは、パターンがランダムではありません。120より大きなサンプルサイズに対して、サンプルサイズの増加に伴ってDPUが増加しています。この結果は、サンプルサイズと欠陥率の間に相関がある可能性を示しています。したがって、データはポアソン分布に従っておらず、ポアソン工程能力分析を使用して信頼性の高い評価を行うことができません。
ヒストグラム
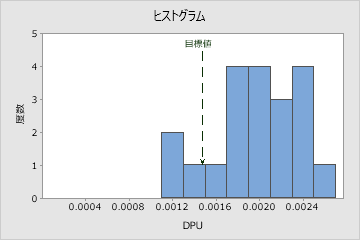
解釈
サンプルの測定単位あたりの欠陥数の分布を評価するには、DPUヒストグラムの分布を使用します。
単位あたりの欠陥数の分布のピークと広がりを調べます。ピークは、最も一般的な値を表し、単位あたりの欠陥数の中心付近にあります。広がりを評価すると、サンプル全体で単位あたりの欠陥数がどの程度変動するかを理解できます。
目標値の参照ラインをヒストグラムのバーと比較します。工程に十分な能力がある場合、ヒストグラムのほとんどまたはすべてのバーが目標値より左側にあります。
DPU平均値
単位あたりの欠陥数(DPU)平均値は、サンプルの測定単位あたりの平均欠陥数です。
解釈
各単位の平均欠陥数の期待値を推定したり、工程が顧客の期待を満たしているかどうかを判断するには、DPUの平均値を使用します。
DPU平均値をDPU目標値と比較して、工程が要件を満たしているかどうかを調べます。DPU平均値が目標値よりも大きい場合、工程を改善する必要があります。
さらに、目標値をDPUに対する信頼区間の上限とも比較する必要があります。信頼区間の上限が目標値よりも高い場合、工程のDPUが目標値より小さいことを確信できません。工程が目標通りかどうかを確信をもって判断するには、より大きなサンプルサイズが必要である可能性があります。
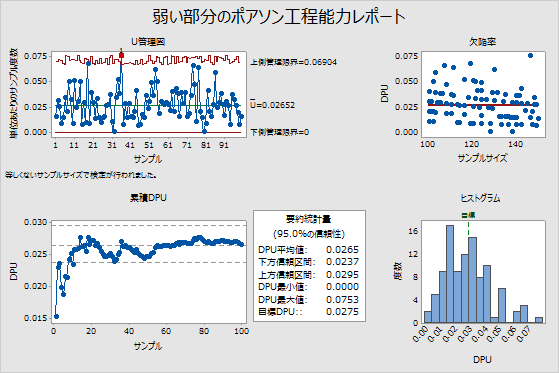
たとえば、次の出力の要約統計量表で、DPU平均値(0.0265)は目標値(0.0275)より小さくなっています。ただし、信頼区間の上限は0.0295で、目標値より大きくなっています。工程は要件を満たしていますが、DPUが目標値より小さいかどうかをより確信をもって判断するには、より大きなサンプルサイズが必要です。
信頼区間(CI)
信頼区間は、工程能力インデックスの起こりうる値の範囲です。信頼区間は、下限と上限によって定義されます。限界値は、サンプル推定値の誤差幅を算定することによって計算されます。下側信頼限界により、工程能力インデックスがそれより大きくなる可能性が高い値が定義されます。上側信頼限界により、工程能力インデックスがそれより小さくなる可能性が高い値が定義されます。
Minitabでは、DPU平均値に対して、下側信頼限界と上側信頼限界の両方が表示されます。
解釈
データのサンプルはランダムであるため、工程から収集された異なるサンプルによって同一の工程能力インデックス推定値が算出されることはまずありません。工程の工程能力インデックスの実際の値を計算するには、工程で生産されるすべての品目のデータを分析する必要がありますが、それは現実的ではありません。代わりに、信頼区間を使用して、工程能力インデックスの可能性の高い値の範囲を算定することができます。
信頼水準が95%の場合は、工程能力インデックスの実際値が信頼区間に含まれるということを95%の信頼度で確信できます。つまり、工程から100個のサンプルをランダムに収集する場合、サンプルのおよそ95個において工程能力の実際値が含まれる区間が作成されると期待できます。
信頼区間により、サンプル推定値の実質的な有意性を評価しやすくなります。可能な場合は、信頼限界を、工程の知識または業界の基準に基づくベンチマーク値と比較します。
たとえば、ある製造工程のユニットあたりの欠陥数の最大許容値は0.025%です。ポアソン工程能力分析によってDPU平均値の推定値として0.011%が得られ、これは工程に十分な能力があることを示しています。ただし、DPU平均値の信頼区間の上限は0.029%です。したがって、分析者は、母集団のDPU平均値が最大許容値を超えていないことを95%の信頼度で確信できません。サンプル推定値の信頼区間を狭めるには、より大きなサンプルサイズを使用するか、データ内の変動を低減する必要があります。
DPU最小値
DPU最小値は、すべてのサンプルにおける測定単位あたりの最小欠陥数です。
解釈
各単位の最小欠陥数の期待値を推定したり、工程が顧客の期待を満たしているかどうかを判断するには、DPU最小値を使用します。
DPU最大値
DPU最大値は、すべてのサンプルにおける測定単位あたりの最大欠陥数です。
解釈
各単位の最大欠陥数の期待値を推定したり、工程が顧客の期待を満たしているかどうかを判断するには、DPU最大値を使用します。
DPU目標値
DPU目標値は、許容できる単位あたりの最大欠陥数です。DPU目標値を指定しなかった場合、DPU目標値が0と仮定されます。
解釈
DPU平均値をDPU目標値と比較して、工程が要件を満たしているかどうかを調べます。DPU平均値が目標値よりも大きい場合、工程を改善する必要があります。
さらに、目標値をDPUに対する信頼区間の上限とも比較する必要があります。信頼区間の上限が目標値よりも高い場合、工程のDPUが目標値より小さいことを確信できません。工程が目標通りかどうかを確信をもって判断するには、より大きなサンプルサイズが必要である可能性があります。

たとえば、要約統計量表で、DPU平均値(0.0265)は目標値(0.0275)より小さくなっています。ただし、DPUに対する信頼区間の上限は0.0295で、目標値より大きくなっています。工程は要件を満たしているように見えますが、DPUが目標値より小さいかどうかをより確信をもって判断するには、より大きなサンプルサイズが必要です。
