このトピックの内容
期待されるサブグループ間・内性能のPPM < LSL
PPM < LSLおよび% < LSLはこの確率の倍数です。
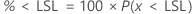
両側信頼区間
P(x < LSL)の信頼区間は次式で求められます。
ここで
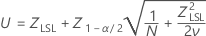
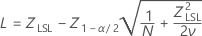
PPM < LSLおよび% < LSLの信頼区間は、この確率の信頼区間に定数を掛けて求められます。
PPM
%
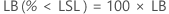
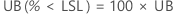
片側信頼限界
片側限界の計算は以下に従います。
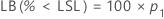
Minitabでは次の式を解き、p1を求めます。
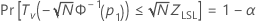
ここで
表記
表記
| 用語 | 説明 |
|---|---|
| LSL | 下側規格限界 |
| USL | 上側規格限界 |
| LB | 下限 |
| UB | 上限 |
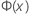 | 標準正規分布の累積分布関数（CDF） |
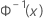 | 標準正規分布の逆累積分布関数（ICDF） |
 | 標準正規分布の第(1 - α/2)百分位数 |
| α | 信頼水準のアルファ |
 | 工程平均（サンプル日付または過去の値から推定される） |
| s | サブグループ間・内のサンプル標準偏差 |
| N | 測定値の個数合計 |
| υ | sの自由度 |
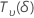 | 以下を使用して非心t分布として分布されたランダム変数 自由度と非心パラメータδ |
期待されるサブグループ間・内性能のPPM > USL
上側規格限界を上回る100万個当たりの部品（PPM > USL）と上側規格限界を上回るパーセント(% > USL)はいずれも、部品が規格限界を上回る確率から求められます（P(x > USL)）。
PPM > USLおよび% > USLはこの確率の倍数です。
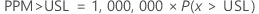
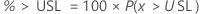
両側信頼区間
P(x > USL)の信頼区間は次式で求められます。
ここで
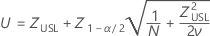
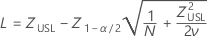
PPM > USLおよび% > USLの信頼区間は、この確率の信頼区間に定数を掛けて求められます。
PPM
%
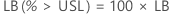
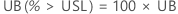
片側信頼限界
片側限界の計算は以下に従います。
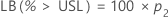
Minitabでは次の式を解き、p1を求めます。
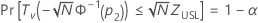
ここで
表記
| 用語 | 説明 |
|---|---|
| USL | 上側規格限界 |
| PPM | 100万個当たりの部品 |
| LB | 下限 |
| UB | 上限 |
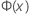 | 標準正規分布の累積分布関数（CDF） |
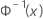 | 標準正規分布の逆累積分布関数（ICDF） |
 | 標準正規分布の第(1 - α/2)百分位数 |
| α | 信頼水準のアルファ |
 | 工程平均（サンプル日付または過去の値から推定される） |
| s | サブグループ間・内のサンプル標準偏差 |
| N | 測定値の個数合計 |
| υ | sの自由度 |
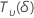 | 以下を使用して非心t分布として分布されたランダム変数 自由度と非心パラメータδ |
期待される「サブグループ間・内」性能のPPM合計
サブグループ間・内の変動に基づき、規格限界外と期待される100万個あたりの部品数は次のとおりです。
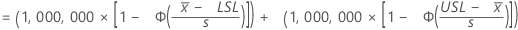
表記
| 用語 | 説明 |
|---|---|
| PPM | PPM(P) |
| LSL | 下側規格限界 |
| USL | 上側規格限界 |
| Φ (X) | 標準正規分布の累積分布関数（CDF） |
 | 観測値の平均 |
| s | サブグループ間・内標準偏差 |
LSLとUSLの両方がわかっている場合の期待されるサブグループ間・内のPPM合計の信頼区間
規格外の100万個当たりの部品（PPM）の合計と規格外のパーセントはいずれも、部品が規格限界外にある確率から求められます。
両側信頼区間
部品が規格外にある確率の上限と下限は次の式で求められます。
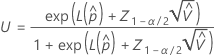
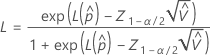
ここで、
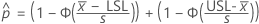
を計算するには、
で、式内のパラメータのサンプル推定値を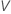 
:
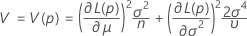
ここで、
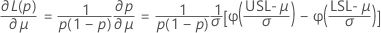
規格外のPPM合計と規格外の合計パーセントの限界は、確率の限界に定数を掛けることで求められます。
PPM
%
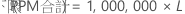
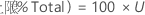
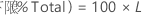
片側信頼限界
部品が規格外にある確率の上限は次の式で求められます。
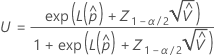
ここで、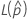
および
は両側区間の場合と同じです。
規格外のPPM合計と規格外の合計パーセントの上限は、確率の限界に定数を掛けることで求められます。
PPM
%
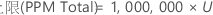
表記
| 用語 | 説明 |
|---|---|
| LSL | 下側規格限界 |
| USL | 上側規格限界 |
| PPM | 100万個当たりの部品 |
| 下限 | 下限 |
| 上限 | 上限 |
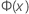 | 標準正規分布の累積分布関数（CDF） |
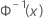 | 標準正規分布の逆累積分布関数（ICDF） |
 | 標準正規分布の確率密度関数 (PDF) |
 | 標準正規分布の第(1 - α / 2)百分位数 |
| α | 信頼水準のアルファ |
 | 工程平均（サンプル日付または過去の値から推定される） |
| s | サブグループ間・内のサンプル標準偏差 |
| N | 測定値の個数合計 |
| υ | sの自由度 |
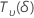 | 非中心T分布として分布する確率変数  自由度と非心のパラメータ δ |
1つの規格限界を持つ工程の期待されるサブグループ間・内のPPM合計の信頼区間
下側規格限界（LSL）のみを持つ工程では、規格外のPPM合計または合計パーセントの信頼区間は、PPM < LSLまたは% < LSLの信頼区間と同じになります。期待されるサブグループ間・内性能についてはPPM < LSLセクションを参照してください。
上側規格限界（USL）のみを持つ工程では、規格外のPPM合計または合計パーセントの信頼区間は、PPM > USLまたは% > USLの信頼区間と同じになります。期待されるサブグループ間・内性能についてはPPM > USLセクションを参照してください。
