LSL
工程の下側規格限界(LSL)は、製品またはサービスの最小許容値です。この制限は、プロセスがどのように実行されているかを示すのではなく、どのように実行するかを示します。LSL は、工程能力分析を設定するときに指定します。
解釈
USLとLSLは、顧客要件を定義し、工程によってその要件を満たす項目が生成されるかどうかを評価するために使用します。
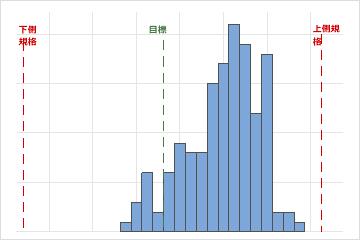
上側規格限界と下側規格限界は、ヒストグラム上の縦破線で識別されます。ヒストグラムバーと線を比較して、測定値が規格限界内にあるかどうかを評価します。
規格広がりは、上側規格限界と下側規格限界の間(USL - LSL)の距離です。ある会社がボールペンを生産する場合、ボールの目標外径が0.35mmだとします。ボール外径の許容範囲は、0.34~0.36mmです。したがって、LSLは0.34、USLは0.36で、規格広がりは0.02mmとなります。
Minitabでは、規格広がりと工程広がりを比較して工程能力を判断します。
目標値
目標値は、顧客の要件に基づいた工程の理想的な値です。たとえば、円筒形の部品が、直径が32mmのときに製品で最適性能を発揮する場合は、32mmがこの部品の目標値となります。
解釈
目標値は、顧客要件を定義し、観測値と比較するために使用します。
目標値は、通常(必ずではない)下側規格限界と上側規格限界の中心に位置します。目標値がある場合は、目標値の近くで工程が中心化されるかどうかを調べます。
USL
工程の上側規格限界(USL)は、製品またはサービスの最大許容値です。この制限は、プロセスがどのように実行されているかを示すのではなく、どのように実行するかを示します。USL は、工程能力分析を設定するときに指定します。

解釈
USLとLSLは、顧客要件を定義し、工程によってその要件を満たす項目が生成されるかどうかを評価するために使用します。
上側規格限界と下側規格限界は、ヒストグラム上の縦破線で識別されます。ヒストグラムバーと線を比較して、測定値が規格限界内にあるかどうかを評価します。
規格広がりは、上側規格限界と下側規格限界の間(USL - LSL)の距離です。ある会社がボールペンを生産する場合、ボールの目標外径が0.35mmだとします。ボール外径の許容範囲は、0.34~0.36mmです。したがって、LSLは0.34、USLは0.36で、規格広がりは0.02mmとなります。
Minitabでは、規格広がりと工程広がりを比較して工程能力を判断します。
サンプル中央値
サンプル中央値は、データセットの中点です。この中間点の値は、観測値の半分がその値より上にあり、観測値の半分がその値より下にあるという点です。中央値は、観測値に順位付けし、順位付けされた順序での順位が[N + 1] / 2の観測値を検出することによって算定されます。観測値の数が偶数の場合、その中央値は、N / 2と[N / 2] + 1の順位で順位付けされる観測値の平均値です。
解釈
サンプル中央値を使用して、工程の中央値を推定します。ほとんどのデータでは、中央値は工程からの典型的なデータの適切な推定値です。通常は、中央値を工程目標値に近づける必要があります。
対称的な釣鐘型の分布に従うデータの場合、サンプル平均は通常、工程からの典型的なデータの適切な推定値です。対称的な釣鐘型の分布に従わないデータの場合、サンプル平均が標準データから遠く離れている場合があります。サンプル中央値は、平均が標準データからかけ離れている場合の標準データのより良い表現です。
サンプル平均
サンプル平均は、サンプル測定値の平均です。
解釈
サンプル平均は、工程の平均値を推定するために使用します。通常は、平均を工程目標値に近づける必要があります。
対称的な釣鐘型の分布に従うデータの場合、サンプル平均は通常、工程からの典型的なデータの適切な推定値です。対称的な釣鐘型の分布に従わないデータの場合、サンプル平均が標準データから遠く離れている場合があります。サンプル中央値は、平均が標準データからかけ離れている場合の標準データのより良い表現です。
サンプル標準偏差
サンプル標準偏差は、すべての測定値の標準偏差であり、工程の全体的な変動の推定値です。データが適切に収集されていれば、全体の標準偏差は全身変動のすべての原因を捉えます。その場合、顧客が時間の経過と共に経験するプロセスの実際の変動を表します。
解釈
標準偏差は、散布度、つまり平均からのデータの広がり方を表す最も一般的な測度です。サンプルの標準偏差が大きい場合、データが平均からより広がっていることを示します。通常、同じ工程は、標準偏差が大きい場合よりも標準偏差が小さい方が能力が高くなります。
サンプルサイズ
サンプルサイズ(N)は、データ内の観測値の合計数です。たとえば、サイズが5のサブグループを20収集した場合、サンプルNは100となります。
解釈
Nは、サンプルサイズを評価するために使用します。
通常、サンプルサイズが大きいほど、算出される推定値の信頼性が高くなります。専門家によっては、工程能力分析で少なくとも合計100個の観測値を収集するよう推奨しています。
