このトピックの内容
確率プロット
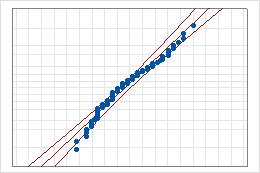
- 中央の線
- パラメータの最尤推定値に基づいて分布で期待される百分位数です。
- 信頼境界線
- 左側の曲線は、百分位数の信頼区間の下側の境界を示します。右側の曲線は、百分位数の信頼区間の上側の境界を示します。
- Anderson-Darling検定の統計量とp値
- 検定の結果により、データが分布に従うかどうかを判定します。
解釈
確率プロットは、各変数の非正規分布の適合度を評価するために使用します。
分布がデータにうまくあてはまる場合は、各点によりほぼ直線が形成されます。この直線から逸脱する場合は、その適合が許容されないことを示します。p値が0.05より大きい場合には、データは分析で使用される非正規分布に従うと仮定することができます。
注
複数の変数について分布が異なる場合は、変数ごとに別々の工程能力分析を実行する必要があります。
工程能力ヒストグラム
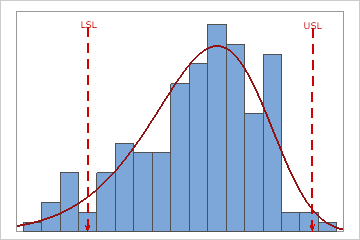
解釈
工程能力ヒストグラムは、分布適合および規格限界とサンプルデータの関係を表示するために使用します。
- 選択した非正規データ分布の不適合の証拠を探す
-
変数ごとに、分布曲線をヒストグラムのバーと比較して、データが分析で選択した分布に従うように見えるかどうかを評価します。バーの曲線からの変動が大きい場合、データは選択した分布に従っておらず、その工程での工程能力の推定値は信頼できない可能性があります。データに最適な分布が不明な場合は、個別の分布の識別を使用して、適切な分布または変換を特定します。
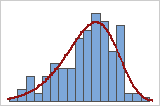
適合度が高い
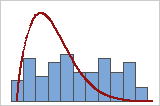
適合度が低い
重要
ヒストグラムによって示されるのは、分布の概ねの適合に過ぎません。分布の適合をより確実に評価するには、確率プロットの結果を使用します。複数の変数について分布が異なる場合は、変数ごとに別々の工程能力分析を実行する必要があります。
- サンプルデータを規格限界と比較する
- 変数ごとに、ヒストグラムでデータと下側および上側規格限界との関係を視覚的に調べます。ヒストグラムでデータと下側および上側規格限界との関係を視覚的に調べます。データの広がりが規格広がりより狭く、すべてのデータが規格限界内にあるのが理想的です。規格限界外のデータは不適合項目を表します。規格限界外の部品がほとんどない、またはまったくないのが理想です。
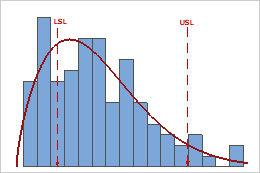
これらの結果では、工程広がりが規格広がりよりも大きく、これは工程能力が低いことを示しています。多くのデータは管理限界内にありますが、下側規格限界(LSL)より低い不適合品や上側規格限界(USL)より高い不適合品が多くあります。
注
工程における不適合品の実際数を調べるには、PPM < LSL、PPM > USL、およびPPM合計の結果を使用します。詳細は、「すべての統計量およびグラフ」を参照してください。
- 工程の位置を評価する
-
変数ごとに、工程が規格限界の間で中心かされているか、または目標値がある場合にはその目標値で中心化されているかどうかを評価します。分布曲線のピークは、ほとんどのデータが存在する位置を示します。
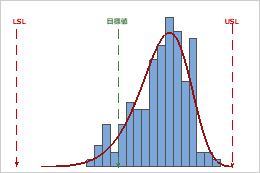
これらの結果では、サンプル観測値は規格限界内にありますが、分布曲線のピークは目標値の位置にありません。ほとんどのデータは目標値を上回り、上側規格限界の近くにあります。
