変数抜取検査（作成・比較）の方法と計算式

目的の方法または計算式を選択してください。

このトピックの内容

サンプルサイズと限界距離
合格確率
不合格確率
平均出検品質（AOQ）

平均検査数（ATI）
合格領域（AR） - デフォルトの手順
合格領域（AR） - Wallis 手順

サンプルサイズと限界距離

サンプルサイズ、n、限界距離、kの計算は、指定された規格限界の数と標準偏差が明らかかどうかによって変わります。

単一規格限界と既知の標準偏差

サンプルサイズは以下で求められます。

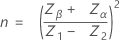
限界距離は以下で求められます。

ここで、

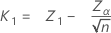
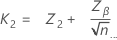
表記

用語	説明
Z₁	標準正規分布の (1 – p₁)* 100 百分位数
p₁	合格品質水準（AQL）
Z₂	標準正規分布の 1 – p₂) * 100 百分位数
p₂	不合格となる品質水準（RQL）
Z_α	標準正規分布の(1 – α) * 100百分位数
α	生産者リスク
Z_β	標準正規分布の(1 – β) * 100百分位数
β	消費者リスク

単一規格限界と未知の標準偏差

表記は単一規格限界と既知の標準偏差と同じです。サンプルサイズは以下で求められます。

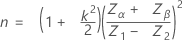
限界距離は以下で求められます。

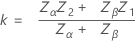
二重規格限界と既知の標準偏差

以下で定義されていない表記は単一規格限界と既知の標準偏差のケースと同じです。まずzが計算されます。

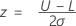
その後、右肩あがりの領域として標準正規分布からp値を見つけます。これは規格限界の範囲外の最小の不良率です。

サンプルサイズと限界距離の計算に使用する方法はp*のこの値によって変わります。

p₁ = AQL、p₂ = RQLとします

2p* ≤ (p₁/ 2)の場合、2つの規格はかなり離れており、計算は単一の規格計画に従います。
₁/ 2 < 2p* ≤ p₁の場合、2つの規格はあまり離れていないもののそれほど近くにあるわけでもないので、不良率の最小値は特定の平均値付近にあります。Minitabでは反復を繰り返して、サンプルサイズと限界距離を見つけます。

次のように定義します。

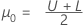
μ = μ₀+ m * h、ここで h = σ/100

m = 1, 2, ...300と仮定します。各μの計算は次のとおりです。

ここでΦは、標準正規分布の累積分布関数です。Prob (X<L) + Prob (X>U)は限りなくp₁に近く、Prob (X<L)とProb (X>U)のうち、大きい方の値を使用して、サンプルサイズと合格数を見つけます。

Prob (X<L)の値が大きいとする場合、p_L = Prob (X<L)と仮定します。

サンプルサイズは以下で求められます。

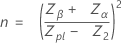
限界距離は以下で求められます。

ここで、

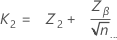
標準正規分布のZ_pL = the (1 – p_L) * 100百分位数

すべてのmの値をすでに使用している一方で対応する確率にp₁が含まれていない場合はp₁が大きすぎ、測定値の平均は区間[L, U]の中点から離れています。こうしたケースでは、単一規格限界およびZ_pL = Z₁の方法を使用できます。Z₁の定義は、単一規格限界のケースと同じです。

p₁< 2p* < p₂の場合、2つの規格限界と標準偏差によって決まる最小不良確率は最小値合格品質水準p₁を上回るので、計画の規格を再検討する必要があります。ロットを不合格にするか、p₁よりも不良率が若干大きい計画を検討することができます。
2p* ≥ p₂2の場合、ロットを不合格にする必要があります。2つの規格限界と標準偏差によって決まる最小不良確率が、拒否品質水準を上回ります。製品を検査せずにロットを不合格にできます。

表記

用語	説明
L	下側規格限界
U	上側規格限界
σ	既知の標準偏差

二重規格限界と未知の標準偏差(デフォルト手順)

表記は前のセクションと同じです。限界距離が、2つの異なる片側限界計画があるケースで設定される値であると仮定します。

サンプルサイズは以下で求められます。

n > 2の場合、次のステップでMSD が計算されます：¹.

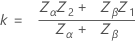
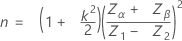
次のように定義します。
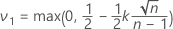
ここで、
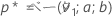
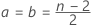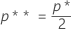
ここでベータは、形状パラメータaおよびbを持つベータ分布の累積分布関数です。ここで、.
ここで、
ここで、ベータ^-1は、ステップ2のベータ分布の逆累積分布関数です。

n ≤ 2の場合、最大標準偏差（MSD）は計算できません。

二重規格限界と未知の標準偏差(Wallis手順)

表記は前のセクションと同じです。手順はSchillingの書籍を参照できます。²

第1限界距離が、2つの異なる片側限界計画があるケースで設定される値であると仮定します。

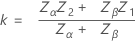
次に、標準正規分布からの右肩あがりの領域 p* を、k に対応する百分位数として検出し、p* / 2の右肩あがりの領域に対応する標準正規分布からの百分位数 Zp** を検出します。

最大標準偏差(MSD)は次の方法で指定されます。

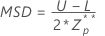
標準偏差の推定値は次のように求められます。

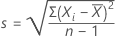
Minitabでは、推定標準偏差 s がMSD以下であるかどうかをテストします。

推定標準偏差 s がMSD以下の場合、サンプルサイズは次の値で指定されます。

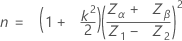
推定標準偏差 s が MSD以上の場合、標準偏差が大きすぎて受入基準と一致しないため、ロットを不合格にする必要があります。

表記

用語	説明
X_i	i番目の測定値
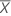	実測値の平均

合格確率

pを、OC曲線上の点のx値である不良率と仮定します。

単一規格限界と既知の標準偏差

単一の下側規格限界と既知の標準偏差: Prob (X < L) = p.
単一の上側規格限界と既知の標準偏差: Prob (X > L) = p.

単一規格限界と未知の標準偏差

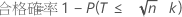
二重規格限界と既知の標準偏差

まずzが計算されます。

その後、右肩あがりの領域としてzに応じて標準正規分布からp値を見つけます。これは規格限界の範囲外の最小の不良率です。

合格確率に使用する方法はp*のこの値によって変わります。

p₁ = AQL、p₂ = RQLと仮定

2p* ≤ (p₁/ 2)の場合、2つの規格はかなり離れており、サンプルサイズと限界距離の計算は単一の規格計画に従います。
p₁/ 2 < 2p* ≤ p₁の場合、2つの規格はあまり離れていないもののそれほど近くにあるわけでもないので、不良率の最小値は特定の平均値付近にあります。

pが任意の場合、グリッド検索アルゴリズムを使用して測定値の平均（μ）を見つけます。

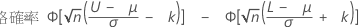
二重規格限界と未知の標準偏差

上側規格限界と下側規格限界の両方があるものの標準偏差がわからない場合、単一限界計画のOC曲線を使用して二重規格限界のケースに近似させます。指定されたp₁、p₂、α、βを持つ単一限界計画から導き出されたOC曲線は、同じp₁、p₂、α、βを持つ両側規格計画のOC曲線の区間の下側限界であり、最も実践的なケースでは、両側計画のOC曲線と見なすこともできます。ダンカン¹を参照してください。

Duncan（1986年）『Quality Control and Industrial Statistics』第5版

表記

用語	説明
n	サンプルサイズ
k	限界距離
σ	既知の標準偏差
Z_p	標準正規分布の第(1 - p)百分位数
Φ	標準正規分布の累積分布関数
T	は自由度 = n - 1および次の非心パラメータを使用した非心t分布です。
L	下側規格限界
U	上側規格限界

不合格確率

不合格確率（P_r）は、特定の抜取計画と入不良比率に基づいて特定のロットを不合格と判定する確率を示します。単純に、1から合格確率を引いた値となります。

P_r = 1 – P_a

ここで、

P_a = 合格確率

平均出検品質（AOQ）

平均出検品質は、検査後の製品の品質水準を表します。平均出検品質は、入不良率の変化に伴って変化します。

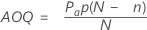
表記

用語	説明
P_a	合格確率
p	入不良率
N	ロットサイズ
n	サンプルサイズ

平均検査数（ATI）

平均検査数は、特定の入検品質水準と合格確率について検査する平均単位数を表します。

表記

用語	説明
P_a	合格確率
N	ロットサイズ
n	サンプルサイズ

合格領域（AR） - デフォルトの手順

合格領域は、両方の仕様が与えられ、標準偏差が不明である場合にのみ計算されます。サンプルサイズと臨界距離のセクションに進み、それぞれn と kの定義を見つけ、方程式の表記を確認します。

合格領域プロットでは、X軸がサンプル平均で、Y軸がサンプル標準偏差です。合格領域は、最大標準偏差（MSD）に加え、サンプル標準偏差およびサンプル平均の3つの関数で構成されています。サンプル標準偏差の値がMSDを越える場合のサンプル平均の値では、合格領域の上側境界がMSDになります。

上側規格限界または下側規格限界の近辺では、合格領域は、次の2の関数で境界が区切られています。

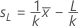
サンプル平均の値が規格限界の中央に近い場合、合格領域の上側境界の座標は以下のステップで計算されます。

次のように定義します。.
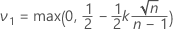次に、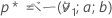ここでベータは、形状パラメータaおよびbを持つベータ分布の累積分布関数です。ここで、.
p₀₂ + p₀₁ = p* を満たす比 p₀₁ および p₀₂のペアを定義します。
次に、

ここで、ベータ^-1は、ステップ2のベータ分布の逆累積分布関数です。
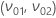、平均と標準偏差の座標の式は以下の通りです。

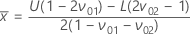
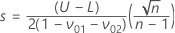
合格領域（AR） - Wallis 手順

以下の計算は、分析に両方の仕様があるが、標準偏差が不明である場合のものです。手順はSchillingの書籍を参照できます。²

このプロットでは、X軸はサンプル平均値を示します(

) Y軸は標準偏差の値を示します。X軸と組み合わせて、以下の線のように合格三角形を形成します。

破線と x 軸は、より正確な領域を形成します。破線を描くには以下の手順を行います。

p* を標準正規分布からの右肩あがりの領域にし、臨界距離をパーセンタイルとします。 P(Z > k).
p₀₂ + p₀₁ = p* を満たす p₀₁および p₀₂の値を選択します。
- p₀₁ = (p* / 100) * h
- p₀₂ = (p* / 100) * (100 - h)
ここで h は 1から00までの値を取ります。
X座標とY座標を定義するには、次の式を使用します。

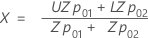
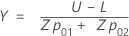
表記

用語	説明
L	下側規格
U	上側規格
k	限界距離
Zp₀₁	標準正規分布の (1 - p₀₁)* 100 百分位数
Zp₀₂	標準正規分布の (1 - p₀₂)* 100 百分位数
p₀₁	(p* / 100) * h
p₀₂	(p* / 100) * (100 – h)

¹ Duncan, A. J. (1986). Quality Control and Industrial Statistics (5th ed.). Homewood, Ill: Irwin.

² Schilling and Neubauer (2009). Acceptance Sampling in Quailty Control (2nd ed.)