標本分布は、ある統計量で取得が見込まれる値のそれぞれが1つの母集団の1つの無作為標本から得られる確率を説明、言い換えると、その大きさの無作為標本すべてのうち何割がその値になるのかを説明します。ブートストラップは、単一の無作為標本から複数の標本を復元することで標本分布を推定する方法です。これらの反復標本は再標本と呼ばれます。それぞれの再標本は元の標本と同じ大きさです。
元の標本は抽出された母集団を表します。したがって、元の標本からの再標本は、母集団から多くの標本を採った場合に得られます。再標本に基づく統計量のブートストラップ分布は、統計量の標本分布を表します。
たとえば、M&M'sチョコレートの青い粒の比率の標本分布を推定するとします。無作為の袋を開けて、M&M'sの102粒に23粒（22.5%）の青い粒があると判定します。この元標本から復元する反復抽出で、母集団がどんな風に見えるかがわかります。再標本を採るには、M&Mを元標本から無作為に選び、色を記録し、M&Mを標本に戻します。これを102回行って（元標本の大きさ）、単一の再抽出を完了します。以下の棒グラフは、元標本からの単一のブートストラップ標本を表しています。
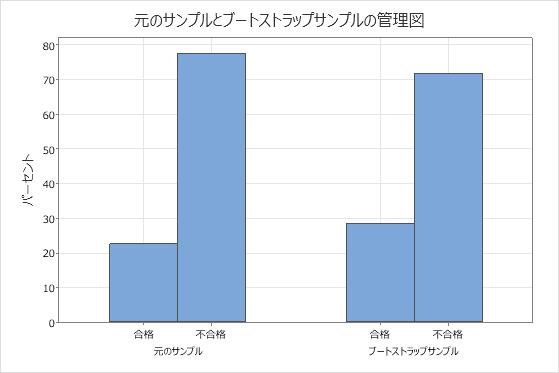
復元抽出法で再抽出が行われたため、ブートストラップ標本の比率が元の比率とぴったり一致することはあまりありません。この棒グラフでは、元抽出でM&M'sの約22.5%が青い粒だとわかったこと、ブートストラップ抽出でM&M'sの約28.4%が青い粒だとわかったことが示されています。ブートストラップ分布を作成するには、再標本をたくさん採ります。以下のヒストグラムは、M&M'sの元の袋の1,000個の再標本のブートストラップ分布を示しています。
ブートストラップ分布は、母比率の推定値である大体22.5%を中心としています。赤い参照線は95%の信頼区間を表しています。ブートストラップ分布の値の中間95%は、青いM&M'sの母比率の95%の信頼区間となります。この例では、95％の信頼度で、青いM&M'sの母比率はおよそ13.7%から31.4%の間に含まれると考えることができます。
ブートストラップと中心極限定理
中心極限定理は、確率と統計の基本的定理です。この定理は
の分布、つまり有限分散を持つ母集団からの無作為標本の平均は、その母集団の分布形状に関係なく、標本の大きさを大きくすると近似的に正規分布になります。ブートストラップを使えば、中心極限定理がいかに作用するかを簡単に理解することができます。指数分布からのデータを考察します。
データが非正規であることは明白です。ですが、50回観測標本を採り、10個の再標本の平均のブートストラップ分布を作成することにします。
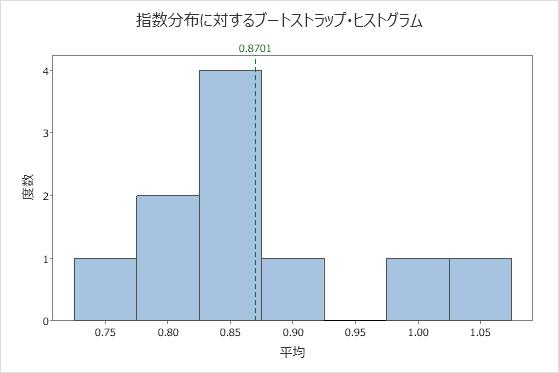
平均分布は指数分布とは大きく異なります。平均分布は正規分布にとても近く見えます。この類似性は、再標本の個数が増えると高まります。1,000個の再標本を使用すると、再標本の平均分布はほぼ正規になります。
