ワイブル分布は、工学、医学的研究、品質管理、金融、および気象学などの幅広い用途のモデル化に使用できる、万能な分布です。たとえば、故障までの時間データをモデル化する信頼性分析でよく使用されます。また、工程能力分析の歪んだ工程データをモデル化するためにも使用されます。
ワイブル分布は、形状、尺度、およびしきい値パラメータによって表され、3-パラメータワイブル分布とも呼ばれます。しきい値パラメータがゼロの場合は、2-パラメータワイブル分布と呼ばれます。2-パラメータワイブル分布は正の変数でのみ定義されます。3-パラメータワイブル分布にはゼロと負のデータを使用できますが、2-パラメータワイブル分布のすべてのデータはゼロより大きくなければなりません。
パラメータの値に応じて、ワイブル分布はさまざまな形状になります。
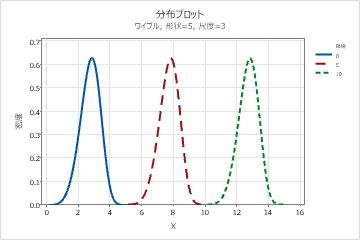
- 形状パラメータの影響
- 形状パラメータは、データがどのように分布するかを表します。3の形状は正規曲線に近似します。1などの低い値の形状は、右方向に歪んだ曲線になります。10などの高い値の形状は、左方向に歪んだ曲線になります。
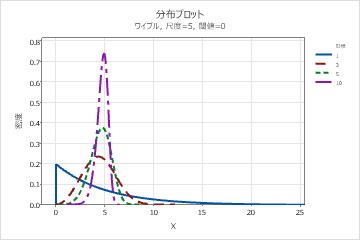
- 尺度パラメータの影響
- 尺度(特性寿命)はデータの63.2%点です。尺度は、しきい値に対するワイブル曲線の位置を定義し、平均が正規曲線の位置を定義する方法と似ています。たとえば、尺度20は、装置の63.2%がしきい値時刻後20時間以内に故障することを示します。
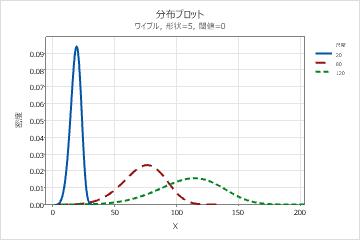
- しきい値パラメータの影響
- しきい値パラメータは、分布の0からのシフトを表します。負のしきい値では分布が左側にシフトし、正のしきい値では分布が右側にシフトします。すべてのデータはしきい値より大きい値である必要があります。2-パラメータワイブル分布は3-パラメータワイブル分布と同じですが、しきい値は0になります。たとえば、3-パラメータワイブル分布(3,100,50)は2-パラメータワイブル分布(3,100)と同じ形状と広がりですが、右側に50単位シフトされます。