ポアソン分布

ポアソン分布は1つのパラメータ（λ）によって指定されます。このパラメータは、平均と分散に相当します。λが十分に大きい値に増加すると、正規分布（λ, λ）を使用してポアソン分布に近似できます。

ポアソン分布を使用すると、有限な観測空間で事象が発生した回数を表すことができます。たとえば、ポアソン分布では、1時間の航空機の機械システムでの欠陥数やコールセンターへの電話の数を表すことができます。ポアソン分布は、品質管理、信頼性/生存時間の調査、および保険の分野などでよく使用されます。

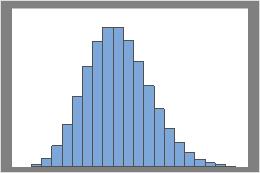
次のグラフは、λが異なるポアソン分布です。

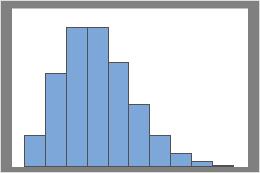
λ = 3

λ = 10

出現率は、平均（λ）を観測空間の次元で割ったものです。これは、異なる観測空間で収集されたポアソンの度数を比較するのに便利です。たとえば、交換台Aで5時間に50件の電話を受けていて、交換台Bで10時間に80件受けているとします。これらの値は異なる観測空間から得られているため、直接比較することができません。これらの度数を比較するには、出現率を計算する必要があります。交換台Aの比率は、（50件/5時間） = 10件/時間です。交換台Bの比率は、（80件/10時間） = 8件/時間です。

ポアソン分布は、事象度数をモデルにするという点で二項分布に似ています。ただし、有限な観測空間内では、ポアソン分布はこの度数に上限を設けていません。交換台は1日のうちに無制限の件数の電話を受けることができ、ポアソン分布の要件に違反しません。対照的に、二項分布では度数に上限があります。観測した事象数は実施した試行数を超えてはいけません。