このトピックの内容
超幾何分布とは
超幾何分布は、サンプル取得元の母集団内の項目総数がわかっている場合に、一定のサンプルサイズにおける事象数をモデル化する離散型分布です。サンプル内の各項目で考えられる結果は、事象または非事象のいずれかです。サンプルは置換が行われないため、サンプル内のすべての項目は異なります。母集団からある項目を選択すると、もう一度それを選択することはできません。したがって、特定の項目がまだ選択されていない場合、それが選択される可能性は試行を重ねるごとに大きくなります。
超幾何分布は、比較的小さな母集団から置換を行わずに抽出されたサンプルに対して使用されます。たとえば、2つの母集団間の差を検定するためのFisherの正確検定、および有限サイズの孤立したロットの計数抜取検査で使用されます。
超幾何分布は、母集団サイズ、母集団での事象計数、およびサンプルサイズという3つのパラメータで定義されます。
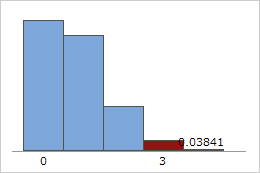
超幾何確率の計算例
試乗できる車が10台あり(N = 10)、そのうち5台にターボエンジンが搭載されているとします(x = 5)。3台の車(n = 3)を試乗した場合、そのうち2台の車がターボエンジンを搭載している確率を調べます。
- を選択します。
- 確率を選択します。
- 母集団サイズ (N)に「10」と入力します。母集団での事象度数 (M)に「5」と入力します。サンプルサイズ (n)に「3」と入力します。
- 定数で入力を選択し、「2」と入力します。
- OKをクリックします。
10台の車のうち3台をランダムに選択して試乗する場合、そのうち2台の車にターボエンジンが搭載されている確率は41.67%です。
超幾何分布と二項分布の違い
超幾何分布と二項分布ではどちらも、固定した試行数で事象が起こる回数が説明されます。二項分布の場合、すべての試行の確率は同じです。超幾何分布の場合は、置換されないので、試行ごとに次の試行の確率が変化します。
二項分布は、母集団が非常に大きいため、次の結果が事象または非事象である確率が試行の結果によってほとんど影響されない場合に使用します。たとえば、100,000人の母集団で、53,000人の血液型がO型だとします。サンプル内で最初にランダムに選択した人物がO型である確率は0.530000です。サンプル内の最初の人物がO型の場合、2番目の人物もO型である確率は0.529995です。この2つの確率の差は小さいため、ほとんどの場合無視できます。
超幾何分布は、母集団が非常に小さいため、次の結果が事象または非事象である確率が試行の結果によって大きく影響される場合に使用します。たとえば、10人の母集団で、7人の血液型がO型だとします。サンプル内で最初にランダムに選択した人物がO型である確率は0.70です。サンプル内の最初の人物がO型の場合、2番目の人物もO型である確率は0.66667です。サンプル数が増えるにつれて、この差は大きくなります。この2つの確率の差は非常に大きいため、多くの場合無視できません。
