メニューから選択した分布のデータに対する確率密度関数、累積分布関数、または逆累積確率を計算することができます。
- 確率分布関数(PDF)
- 確率分布関数(PDF)の曲線は、確率変数の値において高い確率と低い確率を表す領域を示します。たとえば正規分布の場合、最も高いPDF値が平均の位置にある一方、分布の両裾に向かってPDF値が低くなります。
- 累積分布関数(CDF)
- 累積分布関数(CDF)では、指定した変数の値まで累積確率を計算します。CDFを使用して、母集団から取得されたランダム観測値が特定の値以下である確率を判断します。たとえば、累積分布関数では、森の中にある直径の測定値が10インチ以下の木の割合を表示できます。
- 逆累積分布関数(ICDF)
- 逆累積分布関数(ICDF)では、特定の累積確率に関連する変数の値を計算します。たとえば、信頼性技術者が特定の部品の比率が故障するまでの時間を判断するとします。ICDFを使用して、故障時間分布の第95百分位数を判断できます。
連続分布の例

確率密度関数
xがわかっており、それに対応する曲線上の値yを求める場合は、確率密度関数を使用します。
累積分布関数
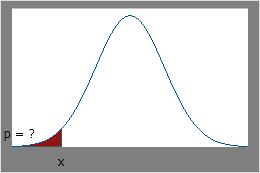
xがわかっており、曲線の下の面積を求める場合は、累積分布関数を使用します。
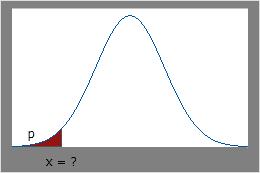
逆累積分布関数
曲線の下の累積面積がわかっており、x値を求める場合は、逆累積分布関数を使用します。
