保証期間を決定する場合のICDFの使用例
たとえば、家電メーカーが自社製トースターの発熱体の故障時間を調べるとします。発熱体の各部分の故障時間を特定することで、保証期間を決めたいと考えています。発熱体の故障時間は、平均値1000時間で正規分布に従い、標準偏差は300時間でした。確率密度関数(PDF)の曲線は、故障の確率が高い領域と低い領域を特定するのに役立ちます。逆CDFは、各累積確率に対応する故障時間を示します。
逆CDFを使って、加熱要素の5%が故障する時間、全加熱要素の95%が故障する時間、または加熱要素の5%だけが残る時刻を推定します。特定の累積確率に対する逆CDFは、PDF曲線下の陰部右側の破壊時間に等しいです。
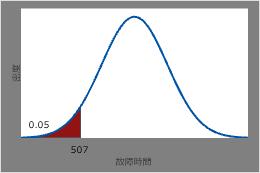
5%が故障するまでの時間を調べる
- を選択します。
- 逆累積確率を選択します。平均に、1000と入力します。標準偏差に、300と入力します。定数で入力に、0.05と入力します。
- OKをクリックします。
加熱要素の5%が故障すると予想される時間は、逆CDFの0.05時間、すなわち506.544時間です。
このプロットは逆CDFを示しています。
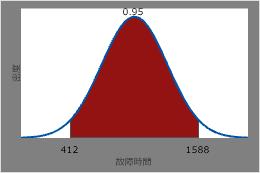
95%が故障する間隔を調べる
- を選択します。
- 逆累積確率を選択します。平均に、1000と入力します。標準偏差に、300と入力します。定数で入力に、0.025と入力します。OKをクリックします。
加熱要素の2.5%が故障すると予想される時間は、逆CDFの0.025時間、すなわち412時間です。
- ステップ2に戻り、「0.025」の代わりに「0.975」と入力します。OKをクリックします。加熱要素の97.5%が故障すると予想される時間は、逆CDFの0.975時間、すなわち1588時間です。
したがって、全加熱素子の95%が故障すると予想される時間帯は、逆CDFが0.025、逆CDFが0.975、すなわち412時間から1588時間となります。
このプロットは逆CDFを示しています。
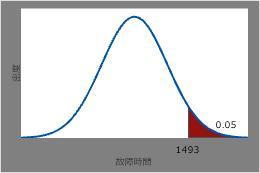
5%が正常に動作し続ける時間を調べる
- を選択します。
- 逆累積確率を選択します。平均に、1000と入力します。標準偏差に、300と入力します。定数で入力に、0.95と入力します。
- OKをクリックします。
加熱素子の5%のみが残ると予想される時間は、逆CDFの0.95、つまり1493時間です。
このプロットは逆CDFを示しています。
超幾何分布でのCDFとICDFの使用例
離散型分布の逆累積確率を求める場合、出力には2つの列セットが含まれます。
逆累積確率の比率pがあるとします。出力の最初の列は、P(X ≤ x) ≤ p となる最大の x を列挙しています。2番目の列は、P(X ≤ x) ≥ p となる最小の x を列挙しています。
超幾何分布の累積確率を計算する
- ワークシートの列C1に 0 1 2を入力してください。
C1 0 1 2 - を選択します。
- 累積確率を選択します。
- 母集団サイズ (N)では、タイプ 20000。
- 母集団での事象度数 (M)では、タイプ 2000。
- サンプルサイズ (n)では、タイプ 20。
- 列から入力 を選んで C1を入力してください。OKをクリックします。
累積分布関数
- P(X ≤ 0) = 0.121448。欠陥数が0の確率は約12%です。
- P(X ≤ 1) = 0.391619。欠陥数が0または1の確率は約39%です。
- P(X ≤ 2) = 0.676941。欠陥数が0、1、または2の確率は約68%です。
超幾何分布の逆累積確率を計算する
欠陥数に関する累積確率が判明したため、逆累積確率を計算します。
累積確率pが0.50の場合の欠陥数xを計算するとします。以前の結果から、P(X ≤ 1 ) = 0.391619、P(X ≤ 2 ) = 0.676941であることがわかっています。超幾何分布は離散分布であるため、欠陥の数は1から2の間にはなり得ません。つまり、欠陥が1つあるか2つあるかもしれませんが、1.4個の欠陥はありえません。したがって、 定数で入力 を選んで 0.50と入力すると、Minitabは出力時に両方の確率を計算します。以下の例に示されています:
- を選択します。
- 逆累積確率を選択します。
- 母集団サイズ (N)では、タイプ 20000。
- 母集団での事象度数 (M)では、タイプ 2000。
- サンプルサイズ (n)では、タイプ 20。
- 定数で入力を選び、 0.50と入力してください。OKをクリックします。
逆累積分布関数
最初の確率は、Xの値を示し、P(X ≤ x) < p and the second probability indicates the smallest x such that P(X ≤ x) ≥ p. In this example, the first probability shows the largest number of defectives, x = 2, such that P(X ≤ 2) <0.5 and the 2nd は欠陥物の最小数 x = 3 を示し、P(X ≤ 3) ≥ 0.5 となります。
ICDFを使用して棄却値を計算する
表を調べる代わりに、Minitabを使用して仮説検定の棄却値を計算することができます。
α=0.02で自由度が12のカイ二乗検定を実行するとします。ここでは、これに対応する棄却値を計算します。α=0.02ということは、累積確率値が1-0.02=0.98となります。
- を選択します。
- 逆累積確率を選択します。
- 自由度に、12と入力します。
- 定数で入力 を選んで 0.98と入力してください。
- OKをクリックします。
Minitabに棄却値24.054が表示されています。カイ二乗検定では、検定統計量が棄却値より大きい場合に、帰無仮説を棄却する統計的証拠があるという結論を下すことができます。
注
この例ではカイ二乗分布を使用しています。ただし、選択した分布で同じ手順に従います。
