連続分布とは
連続分布とは、連続ランダム変数が取り得る値の確率を表します。連続ランダム変数とは、考えられる値のセット(範囲と呼ばれる)が無限で不可算であるランダム変数のことです。
連続ランダム変数(X)の確率は、そのPDFの曲線の下にある領域として定義されます。したがって、値の範囲のみが非ゼロ確率を持てます。連続ランダム変数が特定の値と等しくなる確率は常にゼロです。
体重の分布例
連続正規分布を使用して、成人男性の体重の分布を表すことができます。たとえば、ある男性の体重が160ポンドと170ポンドの間である確率を計算できます。
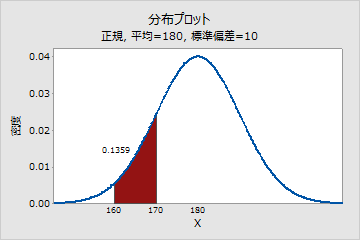
成人男性の体重の分布プロット
この例では、曲線の下の陰影領域が160~170ポンドの範囲を表しています。この範囲の領域は0.136であるため、ランダムに選択した男性の体重が160~170ポンドである確率は13.6%となります。曲線の下側の領域全体は1.0と等しくなります。
しかし、Xが特定の値と正確に等しくなる確率は常にゼロです。これは、幅を持たない単一点での曲線の下側にある領域はゼロであるためです。たとえば、ある男性の体重が無限精度で正確に190ポントである確率はゼロです。男性の体重が190ポンドを超える、190ポンド未満、または189.9~190.1の間であることについてゼロでない確率を計算することはできますが、体重が正確に190ポンドである確率はゼロです。
離散型分布とは
離散型分布は、離散ランダム変数の各値が出現する確率を表します。離散ランダム変数とは、負でない整数のリストなどの数えられる値を持つランダム変数です。
離散確率分布では、離散ランダム変数で取り得る各値をゼロ以外の確率に関連付けることができます。したがって、離散確率分布は多くの場合表形式で表されます。
顧客からの苦情件数の例
| x | P( X = x ) |
|---|---|
| 5 | 0.037833 |
| 10 | 0.125110 |
| 15 | 0.034718 |
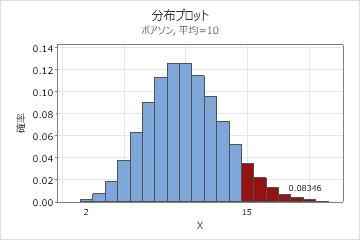
顧客からの苦情件数の分布プロット
この例で陰影の付いたバーは、その日の顧客の苦情件数が15件以上の場合の出現数を表します。バーの高さの和は0.08346であるため、1日あたりの苦情件数が15件以上である確率は8.35%です。
