2標本t検定の無作為化検定を解釈するには、次の手順を実行します。主要な結果には、ヒストグラムとp値が含まれます。
ステップ1:ブートストラップ分布の形状を調べる
ヒストグラムを使用して、ブートストラップ分布の形状を調べます。ブートストラップ分布は、各再標本から選択された統計量の分布です。ブートストラップ分布は、正規分布のように見えるべきです。ブートストラップ分布が非正規である場合、ブートストラップの結果を信頼することはできません。

50個の再標本

1000個の再標本
分布は通常、再標本数が多いほど割り出しやすくなります。たとえば、このデータでは、50個の再標本で分布が不明確です。1000個の再標本になると、形状はほぼ正規に見えます。
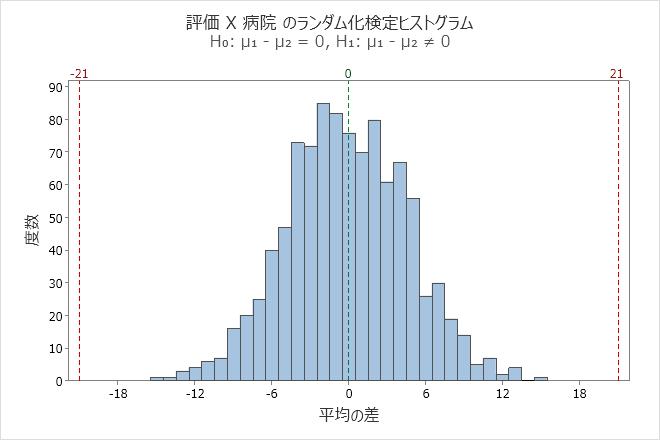
このヒストグラムでは、ブートストラップ分布は正規分布のように見えます。
ステップ2:検定結果が統計的に有意かどうかを判断する
母平均間の差が統計的に有意かどうかを判断するには、p値を有意水準と比較します。通常は、有意水準(αまたはアルファとも呼ばれる)として0.05が適切です。0.05の有意水準は、実際には差が存在しない場合に、差が存在すると結論付けてしまうリスクが5%であるということを示します。
- p値 ≤ α:平均値の間の差は統計的に有意です(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下します。母平均間の差が統計的に有意であると結論付けることができます。信頼区間を計算して差が実質的に有意であるかどうかを判断するには、2サンプル平均のブートストラッピングを使用します。詳細は、統計的有意性と実際的有意性を参照してください。
- p値 > α:平均値の間の差は統計的に有意ではありません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。母平均間の差が統計的に有意であると結論付けるだけの十分な証拠はありません。
方法
| μ₁: 病院 = Aの場合の評価の母平均 |
|---|
| µ₂: 病院 = Bの場合の評価の母平均 |
| 差: μ₁ - µ₂ |
観測されたサンプル
| 病院 | N | 平均 | 標準偏差 | 分散 | 最小 | 中央値 | 最大 |
|---|---|---|---|---|---|---|---|
| A | 20 | 80.30 | 8.18 | 66.96 | 62.00 | 79.00 | 98.00 |
| B | 20 | 59.30 | 12.43 | 154.54 | 35.00 | 58.50 | 89.00 |
観測された平均の差
| Aの平均 - Bの平均 = 21.000 |
|---|
ランダム化検定
| 帰無仮説 | H₀: μ₁ - µ₂ = 0 |
|---|---|
| 対立仮説 | H₁: μ₁ - µ₂ ≠ 0 |
| リサンプル数 | 群平均 | 標準偏差 | p値 |
|---|---|---|---|
| 1000 | -0.185 | 4.728 | < 0.002 |
主要な結果:p値
これらの結果での帰無仮説は、二つの病院間の平均評価の差は0であるという仮説です。p値が有意水準である0.05以下の0.002よりも小さいため、帰無仮説を棄却する決定を下し、病院の評価は異なると結論付けます。
