ヒストグラム
ヒストグラムではサンプル値が多くの区間に分割されており、各区間におけるデータ値の頻度がバーで表されています。
解釈
再標本数50
再標本数1000
分布は通常、再標本数が多いほど判定しやすくなります。例えばこのデータでは再標本数が50の場合だと分布が不明瞭です。再標本数が1000になると、おおよそ正規分布に見えます。
ヒストグラムは仮説検定の結果を可視化して表示します。無作為化標本は、母平均が等しい場合にランダム標本がどのようになるかを表すため、ヒストグラムは0の周りに集中します。片側検定の場合、参照線は元の標本の平均の差の位置に描かれます。両側検定の場合、参照線は元の標本の平均の差の位置と、0を中心として反対側の同じ距離の位置に描かれます。p値は、参照線がある位置の値よりも極端な標本差の比率です。つまり、p値は帰無仮説を真だと仮定した場合に元の標本と同じように極端な標本差の比率ということです。これらの差はヒストグラム上では赤で表示されます。
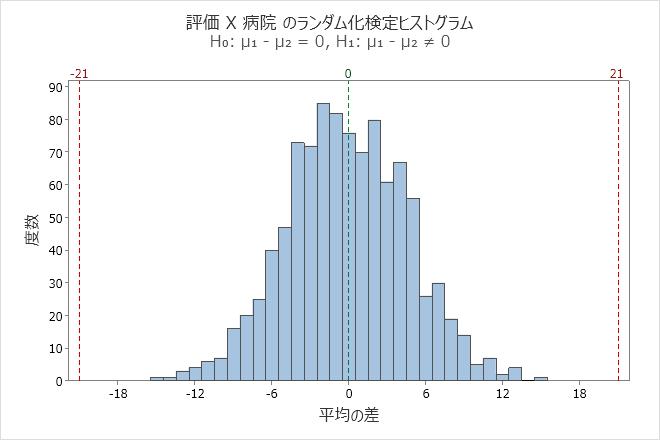
このヒストグラムでは、ブートストラップ分布は正規分布のように見えます。サンプル差が21以上、あるいは-21以下のものはありません。
個別値プロット
個別値プロットは標本内の個別の値を表示します。各円は1つの観測値を表します。個別値プロットは観測値が比較的少なく、各観測値の効果を評価する必要がある場合に特に役立ちます。
注
Minitabでは1回のみ再標本した場合のみ、個別値プロットが表示されます。元のデータと再標本データの両方が表示されます。
解釈
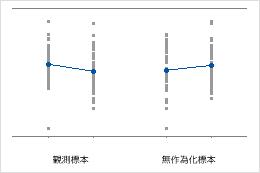
母平均が等しい
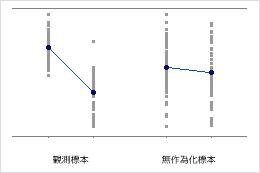
グループ1の母平均がグループ2の母平均の2倍の大きさ
帰無仮説と対立仮説
- 帰無仮説
- 帰無仮説では母集団パラメータ(平均や標準偏差など)は仮説値に等しいと仮定します。帰無仮説とは多くの場合、前回の分析や専門知識を基にした最初の主張を指します。
- 対立仮説
- 対立仮説では、母集団パラメータは帰無仮説の仮説値よりも小さい、大きい、異なると仮定します。対立仮説とは、真であると確信できる、または真であることの証明が期待できる仮説を指します。
方法
| μ₁: 病院 = Aの場合の評価の母平均 |
|---|
| µ₂: 病院 = Bの場合の評価の母平均 |
| 差: μ₁ - µ₂ |
観測されたサンプル
| 病院 | N | 平均 | 標準偏差 | 分散 | 最小 | 中央値 | 最大 |
|---|---|---|---|---|---|---|---|
| A | 20 | 80.30 | 8.18 | 66.96 | 62.00 | 79.00 | 98.00 |
| B | 20 | 59.30 | 12.43 | 154.54 | 35.00 | 58.50 | 89.00 |
観測された平均の差
| Aの平均 - Bの平均 = 21.000 |
|---|
ランダム化検定
| 帰無仮説 | H₀: μ₁ - µ₂ = 0 |
|---|---|
| 対立仮説 | H₁: μ₁ - µ₂ ≠ 0 |
| リサンプル数 | 群平均 | 標準偏差 | p値 |
|---|---|---|---|
| 1000 | -0.185 | 4.728 | < 0.002 |
これらの結果において、帰無仮説は、母集団差が0になるというものです。対立仮説は、その差は0にならないというものです。
再標本数
再標本数は、元のデータセットからMinitabが復元無作為抽出した回数です。通常、再標本数が多いほど上手く機能します。各再標本のサンプルサイズは、元のデータセットのサンプルサイズと等しくなります。再標本数はヒストグラムの観測数と同じです。
平均
平均は、無作為標本の全ての平均の差を合計したものを、再標本数で割ったものです。Minitabでは、平均の差を2つの異なる値で表示します。観測された標本の差とブートストラッピング分布の差(平均)です。どちらの値も、母平均での差の推定値で、通常似た値になります。2つの値が大きく異なっている場合は、元の標本のサンプルサイズを大きくしてください。
標準偏差(ブートストラップ標本)
標準偏差とは、散布度、つまり平均を中心としたデータの広がり方を表す最も一般的な測度です。記号σ(シグマ)は、母集団の標準偏差を示す場合によく使用されますが、sはサンプルの標準偏差を示す場合にも使用されます。多くの場合、工程に対してランダム(自然)な変動は雑音と呼ばれます。標準偏差の単位はデータの単位と同じであるため、通常は、分散よりも解釈が簡単です。
ブートストラップ標本の標準偏差(ブートストラップ標準誤差とも呼ばれます)は、平均の差のサンプル分布で推定される標準偏差です。
解釈
標準偏差を使用して、差の全体平均からのブートストラップ標本の差の拡散程度を判断します。標準偏差の値が高いほど、差の広がりが大きいことを示します。正規分布の経験則によれば、値のおよそ68%が差の全体平均の1つの標準偏差の範囲内にあり、値の95%が2つの標準偏差の範囲内にあり、値の99.7%が3つの標準偏差の範囲内にあります。
ブートストラップ標本の標準偏差から、ブートストラップ標本からの差によって推定される平均の母集団差の正確さを判定します。値が小さいほど、母集団差の推定値の精度が高いことを示します。通常、標準偏差が大きいと、ブートストラップの標準誤差が大きくなり、母集団差の推定値の精度が低くなります。サンプルサイズが大きいと、ブートストラップの標準誤差が小さくなり、母集団差の推定値の精度が高くなります。
p値
p値は帰無仮説を真だと仮定した場合に元のサンプルと同じように極端なサンプル差の比率です。p値が小さいほど、帰無仮説を棄却するための強力な証拠となります。
解釈
- p値 ≤ α:平均値の間の差は統計的に有意です(H0を棄却する)
- p値が有意水準以下の場合は、帰無仮説を棄却する決定を下します。母平均間の差が統計的に有意であると結論付けることができます。信頼区間を計算して差が実質的に有意であるかどうかを判断するには、2サンプル平均のブートストラッピングを使用します。詳細は、統計的有意性と実際的有意性を参照してください。
- p値 > α:平均値の間の差は統計的に有意ではありません(H0を棄却しない)
- p値が有意水準よりも大きい場合は、帰無仮説を棄却しない決定を下します。母平均間の差が統計的に有意であると結論付けるだけの十分な証拠はありません。
