ある医療コンサルタントが2つの病院の患者満足度評価を比較しようとしています。2標本平均の無作為化検定を行って、病院の患者満足度に差があるかを判定してみます。
- 標本データを開く、 病院比較.MWX.
- を選択します。
- 標本で、評価と入力します。
- 標本IDで、病院と入力します。
- オプションをクリックします。乱数ジェネレータの初期値に1を入力します。
注
乱数ジェネレータの初期値を使用して、結果が例と一致することを確認します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
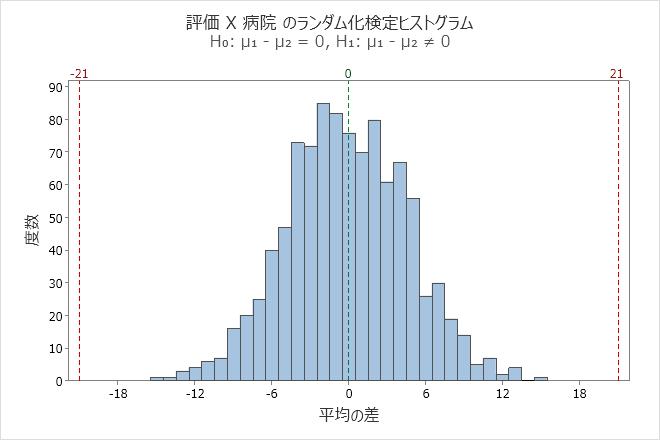
帰無仮説では、病院の患者満足度の差が0に等しいです。p値が0.002で有意水準の0.05より小さいため、医療コンサルタントは帰無仮説を棄却し、病院の患者満足度の差は0に等しくないと結論付けます。ヒストグラムでは、ブートストラップ分布が正規分布に見えるため、医療コンサルタントは結果を信じることができます。
観測平均値の差は21で、病院Aの患者満足度は病院Bよりも高いことを示しています。
方法
| μ₁: 病院 = Aの場合の評価の母平均 |
|---|
| µ₂: 病院 = Bの場合の評価の母平均 |
|---|
| 差: μ₁ - µ₂ |
|---|
観測されたサンプル
| A | 20 | 80.30 | 8.18 | 66.96 | 62.00 | 79.00 | 98.00 |
|---|
| B | 20 | 59.30 | 12.43 | 154.54 | 35.00 | 58.50 | 89.00 |
|---|
ランダム化検定
| 帰無仮説 | H₀: μ₁ - µ₂ = 0 |
|---|
| 対立仮説 | H₁: μ₁ - µ₂ ≠ 0 |
|---|

