このトピックの内容
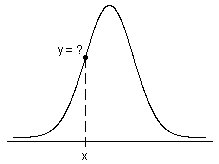
確率密度関数
- 連続分布の場合、Xに区間(a, b)内の値がある確率は、そのPDFの下側の区間(a, b)内の領域です。
- 離散型分布の場合、Xに区間(a, b)内の値がある確率は、(a, b)内でXが取り得る離散値のPDF(確率質量関数)の和です。
累積分布関数
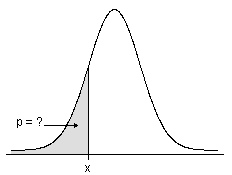
- 連続分布の場合、CDFは確率密度関数の下側の指定したx値までの領域を表します。
- 離散型分布の場合、CDFは指定したx値の累積確率を表します。
逆累積確率
閉区間[0,1]の数pで、確率変数Xの逆累積分布関数(ICDF)は、可能な場合に、X ≤ xの確率がp以上になるように値xを出します。
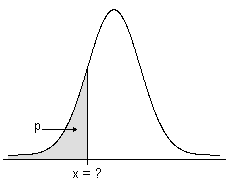
- 連続分布の逆累積分布関数
-
逆累積分布関数は、確率密度関数の下の領域に関連する値です。逆累積分布関数は、値に関連する領域である累積分布関数(CDF)の逆です。
すべての連続分布で、逆累積分布関数が存在し、0 < p < 1である場合に一意です。
- 確率密度関数(PDF)が実数行全体(通常のPDFなど)で正の場合、逆累積分布関数はp = 0またはp = 1のどちらでも定義されません。
- 確率密度関数がある値(カイ二乗PDFなど)より大きいすべての値で正の場合、逆累積分布関数はp = 0で定義されますが、p = 1では定義されません。
- 確率密度関数が区間(一様確率密度関数など)でのみ正の場合、逆累積分布関数はp = 0およびp = 1で定義されます。
- 逆累積分布関数が定義されない場合は、欠損値(*)が結果として返されます。
- 離散型分布の逆累積分布関数
- 逆累積分布関数は、離散型分布に対しては、連続分布に対してよりも複雑です。n = 5、p = 0.4といった二項の累積分布関数を計算する時、累積分布関数が0.5になるような値xはありません。x = 1では、累積分布関数は0.3370です。x = 2では、累積分布関数は0.6826へと増えます。
ベータ分布
ベータ分布は、自然な下限と上限で工程を表すためによく使用されます。
計算式
確率密度関数(PDF)の計算式は次のとおりです。

表記
| 用語 | 説明 |
|---|---|
| α | 形状パラメータ1 |
| β | 形状パラメータ2 |
| Γ | ガンマ関数 |
| a | 下側限界 |
| b | 上側限界 |
a = 0、b = 1の場合、
PDFは次のとおりです。
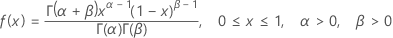


二項分布
二項分布は、n回の独立試行で発生する事象数を表すために使用されます。取り得る値は0~nの整数です。
計算式
平均= np
分散= np(1 – p)
確率質量関数(PMF)の計算式は次のとおりです。
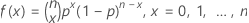
ここで、 =
=  です。
です。
一般に、k!は次のように計算できます。
表記
| 用語 | 説明 |
|---|---|
| n | 試行回数 |
| x | 事象数 |
| p | 事象確率 |
Cauchy分布
Cauchy分布はゼロを中心に左右対称ですが、両裾は正規分布よりも早くゼロに近づきます。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
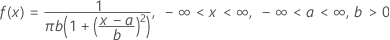
表記
| 用語 | 説明 |
|---|---|
| a | 位置パラメータ |
| b | 尺度パラメータ |
| π | π(~3.142) |
注
値を指定しない場合は、a = 0およびb = 1が使用されます。
カイ二乗分布
Xが標準正規分布を持つ場合、X2は自由度が1のカイ二乗分布を持ちます。これは、一般的に使用されるサンプリング分布です。
n個のX2独立変数(Xは標準正規分布を持つ)の和は、自由度がnのカイ二乗分布を持ちます。カイ二乗分布の形状は自由度に依存します。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
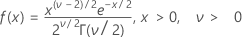
平均= v
分散= 2v
表記
| 用語 | 説明 |
|---|---|
| ν | 自由度 |
| Γ | ガンマ関数 |
| e | 自然対数関数の底 |
離散型分布
離散型分布は自分で定義する分布です。たとえば、3つの値-1、0、1(それぞれの確率が0.2、0.5、および0.3)から成る分布に関心があるとします。ワークシートの列に値を入力すると、それらの列を使用してランダムデータを作成したり、確率を計算したりできます。
| 値 | 確率 |
|---|---|
| −1 | 0.2 |
| 0 | 0.5 |
| 1 | 0.3 |
指数分布
指数分布は、装置の故障の瞬間的な比率(ハザード関数)が一定の場合などに、故障間の時間をモデル化するために使用します。指数分布はワイブル分布とガンマ分布の特殊なケースです。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
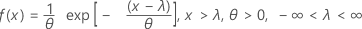
累積分布関数(CDF)の計算式は次のとおりです。

平均= θ + λ
分散= θ2
表記
| 用語 | 説明 |
|---|---|
| θ | 尺度パラメータ |
| λ | しきい値パラメータ |
| exp | 自然対数関数の底 |
注
参考文献によっては、パラメータとして1/θが使用されています。
F分布
F分布は分散比分布とも呼ばれ、分子自由度と分母自由度の2種類の自由度があります。カイ二乗分布を持つ2つの独立確率変数をそれぞれの自由度で割ったものの比の分布です。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
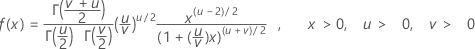

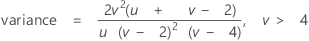
表記
| 用語 | 説明 |
|---|---|
| Γ | ガンマ関数 |
| u | 分子自由度 |
| v | 分母自由度 |
ガンマ分布
ガンマ分布は、正に歪んだデータをモデル化する場合などに使用します。
計算式
確率密度関数(PDF)の計算式は次のとおりです。

平均= ab + θ
分散= ab2
表記
| 用語 | 説明 |
|---|---|
| a | 形状パラメータ(a = 1の場合、ガンマPDFは指数PDFと同じ) |
| b | 尺度パラメータ |
| θ | しきい値パラメータ |
| Γ | ガンマ関数 |
| e | 自然対数関数の底 |
注
参考文献によっては、パラメータとして1/bが使用されています。
幾何分布
離散幾何分布は、確率がpの対象事象を使用した一連の独立したベルヌイ実験に適用されます。
計算式
確率変数Xが確率がpの1つの事象を生成するために必要な合計試行回数である場合、Xの確率質量関数(PMF)は次の計算式で求められます。

Xは次の特性を示します。


確率変数Yが最初の事象(確率がp)を観測する前に発生する非事象数である場合、Yの確率質量関数(PMF)は次の計算式で求められます。

Yは次の特性を示します。


表記
| 用語 | 説明 |
|---|---|
| X | 1つの事象が発生するために必要な試行回数、 Y + 1 |
| Y | 最初の事象より前に発生する非事象数 |
| p | 各試行で事象が発生する確率 |
超幾何分布
超幾何分布は、小さな母集団から置換を行わずに抽出されたサンプルに対して使用されます。たとえば、N台のテレビの出荷があるとします。N1は良品(成功)、N2は不良品(失敗)を示します。交換なしでN台のうちn台のテレビをランダムにサンプル抽出すると、n台のテレビのうちx台が良品である正確な確率がわかります。
計算式
確率質量関数(PMF)の計算式は次のとおりです。
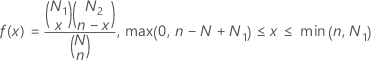


表記
| 用語 | 説明 |
|---|---|
| N | N1 + N2 =母集団サイズ |
| N1 | 母集団での事象数 |
| N2 | 母集団での非事象数 |
| n | サンプルサイズ |
| x | サンプル内の事象数 |
整数分布
整数分布は、整数のセットによる一様分布です。各整数の発生確率は同じです。
正規分布
正規分布(Gaussian分布とも呼ばれる)は最もよく使用される統計的分布です。これは、多くの物理的、生物学的、および社会的な工程をモデル化できるためです。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
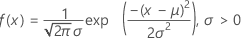
累積分布関数(CDF)の計算式は次のとおりです。
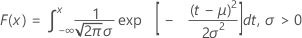
平均= μ
分散= σ 2
標準偏差= σ
表記
| 用語 | 説明 |
|---|---|
| exp | 自然対数関数の底 |
| π | π(~3.142) |
ラプラス分布
ラプラス分布は、分布の頂点が正規分布よりも鋭いときに使用します。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
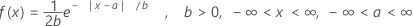
平均= a
分散= 2b2
表記
| 用語 | 説明 |
|---|---|
| a | 位置パラメータ |
| b | 尺度パラメータ |
| e | 自然対数関数の底 |
最大極値分布
最大極値分布を使用すると、分布の最大値をモデル化できます。一連の指数分布があり、X(n)が最初のnの最大値である場合、X(n) – ln(n)は最大極値分布に収束します。したがって、nの値が大きい場合、最大極値分布はX(n) – ln(n)の分布に適切に近似します。
計算式
確率密度関数(PDF)の計算式は次のとおりです。

累積分布関数(CDF)の計算式は次のとおりです。

平均= μ + γσ
分散= π 2 σ 2 / 6
表記
| 用語 | 説明 |
|---|---|
| σ | 尺度パラメータ |
| μ | 位置パラメータ |
| γ | オイラー定数(~0.57722) |
ロジスティック分布
裾部が重くなる点を除いて形状が正規分布に似ている、左右対称な連続分布。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
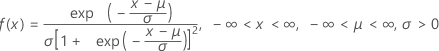
累積分布関数(CDF)の計算式は次のとおりです。
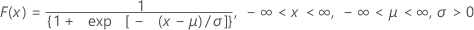
平均= μ
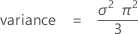
表記
| 用語 | 説明 |
|---|---|
| μ | 位置パラメータ |
| σ | 尺度パラメータ |
対数ロジスティック分布
Y = log(x – λ)がロジスティック分布に従う場合、変数xはしきい値λの対数ロジスティック分布に従います。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
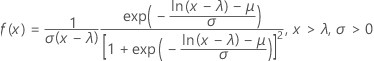
累積分布関数(CDF)の計算式は次のとおりです。

σ < 1の場合

σ < 1/2の場合
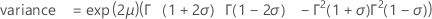
表記
| 用語 | 説明 |
|---|---|
| μ | 位置パラメータ |
| σ | 尺度パラメータ |
| λ | しきい値パラメータ |
| Γ | ガンマ関数 |
| exp | 自然対数関数の底 |
対数正規分布
log(x – λ )が正規分布に従う場合、変数xは対数正規分布に従います。
計算式
確率密度関数(PDF)の計算式は次のとおりです。

累積分布関数(CDF)の計算式は次のとおりです。



表記
| 用語 | 説明 |
|---|---|
| μ | 位置パラメータ |
| σ | 尺度パラメータ |
| λ | しきい値パラメータ |
| π | π(~3.142) |
負の二項分布
負の離散二項分布は、確率がpの対象事象を使用した一連の独立したベルヌイ実験に適用されます。
計算式
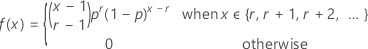


確率変数Yがそれぞれの確率がpのr事象を観測する前に発生する比事象数である場合、Yの確率質量関数(PMF)は次の計算式で求められます。
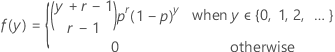
Yは次の特性を示します。


注
負の二項分布は、パスカル分布としても知られています。
表記
| 用語 | 説明 |
|---|---|
| X | Y + r |
| r | 事象数 |
| p | 事象確率 |
ポアソン分布
ポアソン分布は、一定の割合の出現に基づいてある事象数をモデル化する離散型分布です。ポアソン分布は、独立した試行数が大きく成功の確率が低い場合に、二項分布に対する近似として使用できます。
計算式
確率質量関数(PMF)の計算式は次のとおりです。
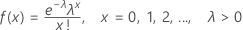
平均 = λ
分散 = λ
表記
| 用語 | 説明 |
|---|---|
| e | 自然対数関数の底 |
最小極値分布
最小極値分布を使用すると、分布の最小値をモデル化できます。Yがワイブル分布に従う場合、log(Y)は最小極値分布に従います。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
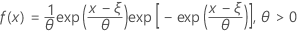
累積分布関数(CDF)の計算式は次のとおりです。



表記
| 用語 | 説明 |
|---|---|
| ξ | 位置パラメータ |
| θ | 尺度パラメータ |
| e | 自然対数関数の底 |
| v | オイラー定数(~0.57722) |
t分布
- 分散が不明なときに、正規分布から母平均の信頼区間を作成する。
- 分散が不明であるが等しい正規母集団から抽出された2つのサンプルの平均が有意に異なるかどうかを判断する。
- 回帰係数の有意性を検定する。
計算式
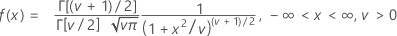
平均= 0、ν > 0の場合

表記
| 用語 | 説明 |
|---|---|
| Γ | ガンマ関数 |
| v | 自由度 |
| π | π(~3.142) |
三角分布
三角分布のPDFの形状は三角形です。
計算式
確率密度関数(PDF)は以下になります。
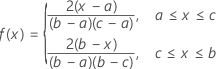

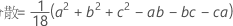
表記
| 用語 | 説明 |
|---|---|
| a | 下側エンドポイント |
| b | 上側エンドポイント |
| c | モード(PDFがピークになる位置です) |
一様分布
一様分布は、最小値としてa、最大値としてbを使用して、均一な区間でデータを特徴付けます。
計算式
確率密度関数(PDF)の計算式は次のとおりです。

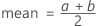

表記
| 用語 | 説明 |
|---|---|
| a | 下側エンドポイント |
| b | 上側エンドポイント |
ワイブル分布
ワイブル分布は、製品の故障時間をモデル化するときに役立ちます。
計算式
確率密度関数(PDF)の計算式は次のとおりです。
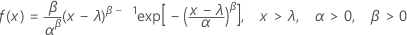
累積分布関数(CDF)の計算式は次のとおりです。

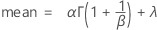
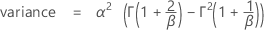
表記
| 用語 | 説明 |
|---|---|
| α | 尺度パラメータ |
| β | 尺度パラメータ(β = 1の場合、ワイブルPDFは指数PDFと同じ) |
| λ | しきい値パラメータ |
| Γ | ガンマ関数 |
| exp | 自然対数関数の底 |
注
参考文献によっては、パラメータとして1/αが使用されています。
