平均
一連の数字の中心として一般的に使用される測度。平均は平均値とも呼ばれます。これは、すべての観測値の和を(非欠損)観測値数で割ったものです。
計算式
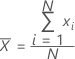
表記
| 用語 | 説明 |
|---|---|
| xi | i番目の観測値 |
| N | 非欠損観測値の数 |
標準偏差
サンプルの標準偏差により、データの広がりの測度が得られます。サンプル分散の平方根に等しくなります。
計算式
 の場合、サンプルの標準偏差は次のようになります。
の場合、サンプルの標準偏差は次のようになります。

表記
| 用語 | 説明 |
|---|---|
| x i | i番目の観測値 |
 | 観測値の平均 |
| N | 非欠損観測値の数 |
分散
分散は、平均を中心としたデータの広がり方を測定します。分散は、標準偏差の二乗に等しくなります。
計算式
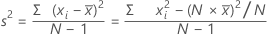
表記
| 用語 | 説明 |
|---|---|
| xi | i番目の観測値 |
 | 観測値の平均 |
| N | 非欠損観測値の数 |
和
計算式

表記
| 用語 | 説明 |
|---|---|
| xi | i番目の観測値 |
最小値
データセットにおける最小の値。
中央値
サンプル中央値は、データの中央にあります。観測値の少なくとも半分は中央値以下、少なくとも半分は中央値以上になります。
N個の値がある列があるとします。中央値を計算するには、最初にデータ値を最小から最大の順に並べます。Nが奇数の場合は、サンプル中央値は中央にある値です。Nが偶数の場合は、サンプル中央値は中央の2つの値の平均です。
たとえば、N = 5でデータx1、x2、x3、x4、およびx5がある場合、中央値 = x3です。
N = 6で順序付きデータx1、x2、x3、x4、x5、およびx6がある場合、次のようになります。

ここで、x3とx4は3番目と4番目の観測値です。
最大値
データセットにおける最大の値。
平均
計算式
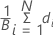
表記
| 用語 | 説明 |
|---|---|
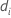 | i番目の再サンプルの平均の差 |
| B | 再サンプル数 |
| N | 元サンプルに含まれるグループの観測数 |
ブートストラッピング分布の標準偏差
計算式

表記
| 用語 | 説明 |
|---|---|
 | 再サンプルの差の平均 |
| B | 再サンプル数 |
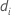 | i番目の再サンプルの平均の差 |
信頼区間
計算式
再標本の平均の差を昇順で並び替えます。d1は最も小さい数字、dBは最も大きい数字です。
下限:dl ここでは、= 
上限:du ここでは、= 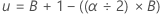
注
片側(下限のみまたは上限のみ)の場合、α/2の代わりにαを使用します。
lまたはuが整数ではない場合、Minitablまたはuのいずれかの側の2つの数字の間で線形補完が実行されます。計算式は以下になります。
dy + z(dy+1 - dy)
たとえば、l = 5.25の場合、下限はd5 + 25(d6 - d5)に等しくなります。
である場合、Minitabでは信頼区間が表示されません。 または
または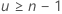 .
.
表記
| 用語 | 説明 |
|---|---|
| α | 1- 信頼区間/100 |
| B | 再標本数 |
| dy | 最小から最大の順に並べ替えられたy番目の差 |
| y | lまたはuの切り捨てられた値 |
| z | l-yまたはu - y |
