2サンプル平均のブートストラッピングのブートストラップ標本の統計量およびグラフ

ヒストグラムではサンプル値が多くの区間に分割されており、各区間におけるデータ値の頻度がバーで表されています。

解釈

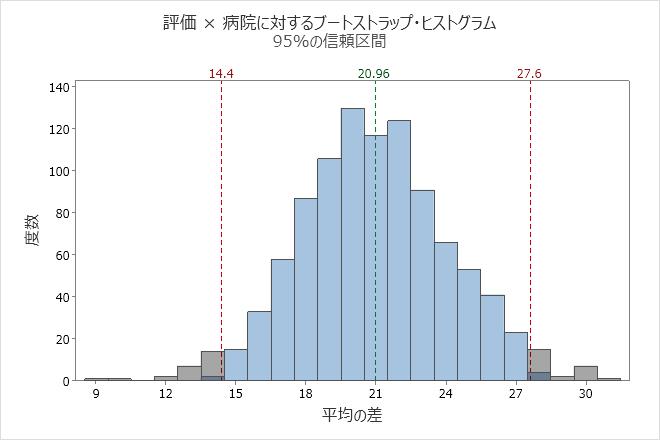
ヒストグラムを使用して、ブートストラップ分布の形状を調べます。ブートストラップ分布は、各再標本の平均の差の分布です。ブートストラップ分布は、正規分布のように見えるべきです。ブートストラップ分布が非正規である場合、結果を信頼することはできません。

50個の再標本

1000個の再標本

個別値プロットは、標本に対して個別の値を表示します。各円は1つの観測値を表しています。個別値プロットは、観測値の数が比較的少ない場合と、各観測値の効果も評価する必要がある場合に、特に有効です。

解釈

標本の大きさが大きい場合、ブートストラップ標本は通常、元の標本と同様の中心と広がりになります。標本の大きさが小さい場合は、元の標本とは異なるブートストラップ標本になる可能性があります。ブートストラップ標本が元の標本と似ていない場合、標本の規模を大きくすることを考える必要があります。

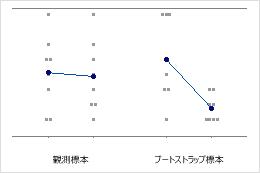
標本の大きさ8

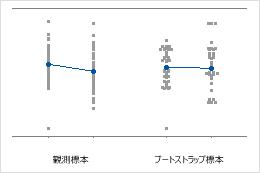
標本の大きさ50

再標本数は、元のデータセットからMinitabが復元無作為抽出した回数です。通常、再標本数が多いほど上手く機能します。各再標本のサンプルサイズは、元のデータセットのサンプルサイズと等しくなります。再標本数はヒストグラムの観測数と同じです。

平均は、ブートストラップ標本の平均の差すべての和を再標本数で割ったものです。

標準偏差とは、散布度、つまり平均を中心としたデータの広がり方を表す最も一般的な測度です。記号σ（シグマ）は、母集団の標準偏差を示す場合によく使用されますが、sはサンプルの標準偏差を示す場合にも使用されます。多くの場合、工程に対してランダム（自然）な変動は雑音と呼ばれます。標準偏差の単位はデータの単位と同じであるため、通常は、分散よりも解釈が簡単です。

ブートストラップ標本の標準偏差（ブートストラップ標準誤差とも呼ばれます）は、平均の差のサンプル分布で推定される標準偏差です。

信頼区間は、統計量の標本分布に基づいています。統計量にパラメータの推定量としての偏りがない場合、標本分布はパラメータの真の値を中心とします。ブートストラッピング分布は、統計量の標本分布に近似します。したがって、ブートストラッピング分布の値の中間95%は、パラメータの95%の信頼区間となります。信頼区間により、母集団パラメータで推定値の実質的な有意性を評価しやすくなります。状況に応じた専門知識を利用して、信頼区間に実質的に有意な値が含まれているかどうかを判断します。