確率プロットは、各観測値(反復値を含む)の値を推定累積確率に対比させてプロットすることにより、サンプルから推定累積分布関数(CDF)を作成します。
Minitabでは、で選択したもの(デフォルトは中央値順位)に合わせて、次式の1つを使用して推定された累積確率を計算します。各計算式で、nは観測値の数、iは各観測値の順位を示します。したがって、i = 1が最小値でi = nが最大値になります。
- 中央値順位(ベナード)
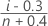
- 平均順位(ハード-ジョンソン)

- 修正されたカプラン-マイヤー(ヘイズン)
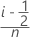
- カプランーマイヤー

注
カプランーマイヤー法により、最大の観測値ではp = 1になります。その結果得られた値は、プロットでは使用されないので、かわりに最大のpを、先行するpと1との距離の90%として計算します。
適合分布線は、指示されたパラメータ(推定値または経験値のいずれか)を持つ、選択した論理的分布の累積分布関数を表します。パラメータの経験値を指定しない場合は、最小二乗推定法(正規分布または対数正規分布)または最尤推定法(その他の分布)を使ってパラメータを推定します。
Y値(場合によってはX値)は、適合ラインが線形になるように変換されます。ただし、目盛ラベルは未変換値と一致するラベルのままです。つまり、選択した分布がデータに適合する限り、プロットされる点は直線を形成します。
次の表は、各分布で使用される変換を示します。
| 分布 | X座標 | Y座標(スコア) |
|---|---|---|
| 正規 | データ | |
| 対数正規 | ln(データ) | |
| 3パラメータ対数正規 | ln(データ~しきい値) | |
| ガンマ | ln(データ) | G-1(p), k |
| 3パラメータガンマ | ln(データ~しきい値) | G-1(p), k |
| 指数 | ln(データ) | ln(-ln(1 - p)) |
| 2パラメータ指数 | ln(データ~しきい値) | ln(-ln(1 - p)) |
| 最小極値 | データ | ln(-ln(1 - p)) |
| ワイブル | ln(データ) | ln(-ln(1 - p)) |
| 3パラメータワイブル | ln(データ~しきい値) | ln(-ln(1 - p)) |
| 最大極値 | データ | -ln(-ln(p)) |
| ロジスティック | データ |
 |
| 対数ロジスティック | ln(データ) |
 |
| 3パラメータ対数ロジスティック | ln(データ~しきい値) |
 |
重要
しきい値に対して調整されていないデータをプロットする場合、適合度は直線では示されません。
表記
| 用語 | 説明 |
|---|---|
| データ | 観測値のデータ値 |
| In(x) | xの自然対数 |
| 標準正規分布の逆累積分布関数によって返されるpの値 | |
| G-1(p),k | ガンマ分布の逆累積分布関数(形状 = k、尺度 = 1)によってpに値が返ります。経験値を入力しない限り、この推定された形状パラメータが使用されます。 |
