1つのYを持つ折れ線グラフの主要な結果を解釈する

プロットの線が平行でない場合、交互作用があるかもしれません。交互作用は、1番目のＸ変数の水準にあるＹデータの平均は、2番目のＸ変数の水準ごとに異なることを示しています。ラインの非平行度が高いほど、交互作用の強度が高くなります。

次のラインプロットは、4台の機械と3人の作業者により製造された繊維の平均強度を示します。作業者1が機械2を使ったときに生じる平行でない線は、可能な交互作用があることを意味しています。この組み合わせは、予想外の高い平均強度を生み出しているため、追跡調査を行う必要があるといえます。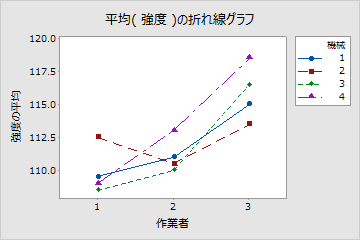

注

ラインプロットを使用すれば効果と交互作用を表示できますが、適切な統計的検定を実行して、確認する効果または交互作用の統計的有意性を評価します。交互作用の効果が有意な場合は、主効果の解釈では必ず交互作用効果も考慮する必要があります。

斜線は、X因子によって起こりうる効果を示します。線と線の差は、凡例の因子によって起こりうる効果を示します。研究対象と関係する可能性のある効果（または効果の欠如）を評価します。

Yの目標

Yを最小化または最大化する、あるいはYの目標値達成に最も近いX変数の水準を確認します。

Xにおいて変化するYの強固さ

他のX変数に対してYを強固にする1つのX変数の水準を確認します。たとえば、グラフのs軸上のX変数のすべての設定、または凡例のX変数のすべての設定においてYの平均はほとんど同じかどうかを特定します。

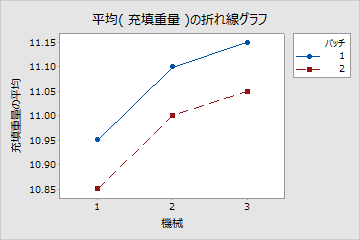
次のラインプロットには、材料の2つのバッチを使用して、3台の機械により製造されたフード製品の充填重量の平均が表示されます。ラインの傾きも0でないことから、機械ごとの平均充填重量が異なることが分かります。機械2は、一般的に11.00の目標となる充填重量に最も近いです。機械1は充填不足になり、機械3は充填過剰になる傾向があります。バッチ2の機械ごとの充填重量は、バッチ1よりも一貫して低くなります。