平滑化ラインについて
平滑化ラインが最も役立つのは、関係の曲面が急激に変化しない場合です。グラフに追加される平滑化ラインはLOWESS平滑化法を使用して計算されます。
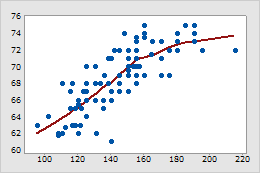
平滑化ラインを使用した散布図
時系列プロットでは、1本の平滑化ラインは実線で、もう1本は点線です。
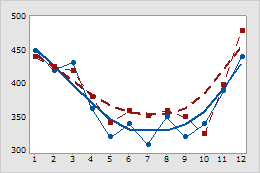
各グループに平滑化ラインを使用した時系列プロット
- LOWESS平滑化パラメータ
-
- 平滑化の次数
- 0~1の値を入力できます。LOWESS平滑化ラインは、通常、点の割合(f)が変数間の基本的な関係を歪めることなく、平滑化による適合を行うのに十分な大きさである場合が最も有効です。クリーブランド Cleveland(1)は、fを可能な限り大きくしつつ、y値の残差対x値の別なLOWESSプロットで関連性のなさを維持することを提案しています。
- ステップ数
- 外れ値の平滑化されたy値への影響を制限するため、平滑化の反復数を設定できます。0~10の値を入力できます。ステップごとに、重み付け線形回帰の次回の反復で外れ値に与えられる重みが減らされます。これは、前のLOWESSステップでの残差の大きさに基づいて実行されます。なお、クリーブランドでは、ほとんどのデータの場合、2回のロバストステップで外れ値の影響を適切に平滑化できると説明されています。
グラフ作成時に平滑化ラインを追加する
- 散布図
- 行列散布図
- 時系列プロット
- ヒストグラム
- グラフ作成ダイアログボックスで、データ表示をクリックします。
- 平滑化をクリックします。
- LOWESSをクリックします。
- (オプション)平滑化の次数に、各x値での適合値の計算に使用される点の総数に対する割合として、0~1の数字を入力します。デフォルトは0.5です。平滑化の次数が小さいほど、平滑化はデータの小さなパターンに従う傾向があります。平滑化の次数が大きいほど、平滑化はデータの全体のパターンに従う傾向があります。
- (オプション)ステップ数に、外れ値の影響を制限するための平滑化の反復数を示す、0~10の数字を入力します。ステップごとに、次回の反復で外れ値に与えられる重みが減らされます。デフォルトは2です。
- OKをクリックします。
グラフに平滑化ラインを追加する
散布図、行列散布図、ヒストグラム、時系列プロットにLOWESS平滑化ラインを追加できます。
- グラフをダブルクリックします。
- グラフを右クリックしてを選択します。
- (オプション)平滑化の次数に、各x値での適合値の計算に使用される点の総数に対する割合として、0~1の数字を入力します。デフォルトは0.5です。平滑化の次数が小さいほど、平滑化はデータの小さなパターンに従う傾向があります。平滑化の次数が大きいほど、平滑化はデータの全体のパターンに従う傾向があります。
- (オプション)ステップ数に、外れ値の影響を制限するための平滑化の反復数を示す、0~10の数字を入力します。ステップごとに、次回の反復で外れ値に与えられる重みが減らされます。デフォルトは2です。
- OKをクリックします。
グラフの平滑化ラインを編集する
平滑化ラインをグラフに追加した後は、色、サイズ、種類、パラメーターを変更できます。
- グラフをダブルクリックします。
- 編集する平滑化ラインをダブルクリックします。 平滑化ラインの選択に関する詳細は、グラフ上のグループおよび単一項目を選択するを参照してください。
- タブを選択して必要な編集を行います。
- 属性:線の色、サイズ、種類を変更します。
- グループ:グループ変数で属性を割り当てます。
- オプション:平滑化の次数と平滑化のステップ数を変更します。
- OKをクリックします。
LOWESS法
LOWESS平滑化法は平滑化ラインを決定するための一般的な手法です。LOWESSはlocally-weighted scatterplot smoother(局所的な重み付けをした散布図平準化)の略です。平滑化の度合いや外れ値からの影響を変更するために、パラメータを指定できます。
LOWESSルーチンは、各x値について、平滑化された新しいy値を計算します。
-
このルーチンは、(x、y)点のいずれかの側のx-値で最も近傍にあるデータを使用して、すべての点の中から一定割合(デフォルトではf = 0.5)の点を選択します。この割合は平滑化の次数と呼ばれます。この選択では、一般的に、X変数値の一方の側から選択された点がもう一方の側からの点よりも多くなります。次の例は、与えられた点に対して選択された一定割合のデータを示しています。影が付けられた領域には、赤色のデータ点に最も近い半数(0.5)の点が保持されています。
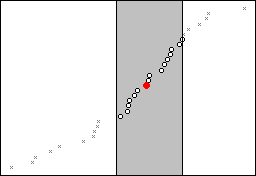
-
Minitabでは、選択した少数部と平滑化する点とのx距離を使用して重みを計算します。

次のグラフは、選択した点の割合の重み(垂直)とX値(水平)の関係を示しています。各x-値に最も近い点が、平滑化で最大の重みを持ちます。

-
ステップ2からの重みを使用して、選択された一定割合のデータのすべての点について重み付け線形回帰が実行され、最初の平滑化された値が生成されます。
-
最終的に、ステップ3の交互作用(デフォルトはn = 2)をさらに使用することにより、外れ値の影響は制限されます。新しい重みは以下の要領で計算されます。

