列統計量および行統計量の結果を解釈する

和とは、すべてのデータ値の合計です。和は、平均や標準偏差などの統計量計算にも使用されます。

平均値は、データの平均であり、すべての観測値の和を観測値の数で割って求められる値です。

たとえば、銀行での5人の顧客の待ち時間が3、2、4、1、2（分）であったとします。この場合、平均待ち時間は次のようにして計算されます。

顧客は、銀行のサービスを受けるために、平均で2.4分間待っていることになります。

解釈

データの中心を表す1つの値でサンプルを表すのに、平均を使います。多くの統計分析では、平均がデータ分布の中央の標準測度として使用されます。

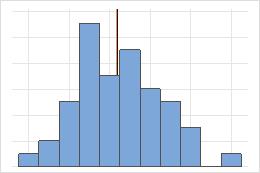
中央値と平均はともに中心化傾向の測度となります。しかし、外れ値と呼ばれる異常な値は、平均に対してよりも小さいですが、中央値に対して影響する可能性があります。データが左右対称である場合、平均と中央値は似ています。

対称

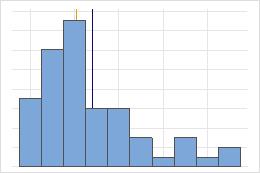
非対称

標準偏差とは、散布度、つまり平均を中心としたデータの広がり方を表す最も一般的な測度です。記号σ（シグマ）は、母集団の標準偏差を示す場合によく使用されますが、sはサンプルの標準偏差を示す場合にも使用されます。多くの場合、工程に対してランダム（自然）な変動は雑音と呼ばれます。

標準偏差の単位はデータの単位と同じであるため、通常は、分散よりも解釈が簡単です。

解釈

標準偏差を使用して、平均からのデータの拡散程度を判断します。 標準偏差の値が高いほど、データの広がりが大きいことを示します。 正規分布の経験則によれば、値のおよそ68%が平均の1つの標準偏差の範囲内にあり、値の95%が2つの標準偏差の範囲内にあり、値の99.7%が3つの標準偏差の範囲内にあります。

標準偏差を使用して、工程の全体的な変動を推定するためのベンチマークを設定することもできます。

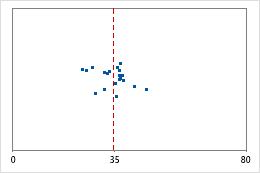
病院1

病院2

最小値とは、最小のデータ値を指します。

このデータで、最小値は7です。

最大値とは、最大のデータ値を指します。

このデータで、最大値は19です。

範囲とは、サンプルの最も大きいデータ値と最も小さいデータ値の差です。範囲は、すべてのデータ値が含まれる区間を表します。

中央値はデータセットの中間点です。この中間点の値は、観測値の半分がその値より上にあり、観測値の半分がその値より下にあるという点です。中央値は、観測値に順位付けし、順位付けされた順序での順位が[N + 1] / 2の観測値を検出することによって算定されます。観測値の数が偶数の場合、その中央値は、N / 2と[N / 2] + 1の順位で順位付けされる観測値の平均値です。

解釈

中央値と平均はともに中心化傾向の測度となります。しかし、外れ値と呼ばれる異常な値は、平均に対してよりも小さいですが、中央値に対して影響する可能性があります。データが左右対称である場合、平均と中央値は似ています。

対称

非対称

未修正の平方和は、列の各値を平方し、その和を計算することで計算されます。たとえば、列にx₁, x₂, ... , x_nが含まれている場合、平方和の計算は（x₁² + x₂² + ... + x_n²）となります。修正された平方和とは異なり、未修正の平方和は誤差を含みます。データ値は最初に平均を引かずに二乗します。

列に含まれる観測値の合計数。欠損値の数と非欠損値の数の和を示すために使用します。

サンプルにおける非欠損値の数。

サンプルにおける欠損値の数。欠損値の数は、欠損値記号*を含むセルを参照します。