The process standard deviation is also called sigma, or σ. If you enter an historical value for sigma, then Minitab uses the historical value. Otherwise, Minitab uses one of the following methods to estimate sigma from the data.
In This Topic
Rbar method
Minitab uses the range of each subgroup, 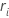 , to calculate
, to calculate 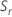 , which is an unbiased estimator of σ:
, which is an unbiased estimator of σ:
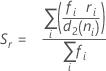
where
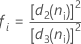
When the subgroup size is constant, the formula simplifies to the following:
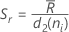
where 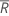 (Rbar) is the mean of the subgroup ranges, calculated as follows:
(Rbar) is the mean of the subgroup ranges, calculated as follows:

Notation
| Term | Description |
|---|---|
| ri | range for subgroup i |
| m | number of subgroups |
| d2(·) | value of unbiasing constant d2 that corresponds to the value specified in parentheses. |
| ni | number of observations in subgroup i |
| d3(·) | value of unbiasing constant d3 that corresponds to the value specified in parentheses. |
Pooled standard deviation method
The pooled standard deviation (Sp) is given by the following formula:
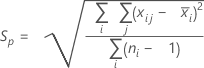
When the subgroup size is constant, Sp can also be calculated as follows:

With unbiasing constant
By default, Minitab applies the unbiasing constant, c4(), when you use the pooled standard deviation to estimate σ:
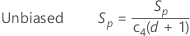
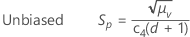
Notation
| Term | Description |
|---|---|
| xij | jth observation in the ith subgroup |
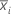 | mean of subgroup i |
| ni | number of observations in subgroup i |
| μv | mean of the subgroup variances |
| c4(·) | value of the unbiasing constant c4 that corresponds to the value that is specified in parentheses. |
| d | degrees of freedom for Sp, given by the following formula:
 |
Unbiasing constants d2(), d3(), and d4()
d2(N) is the expected value of the range of N observations from a normal population with standard deviation = 1. Thus, if r is the range of a sample of N observations from a normal distribution with standard deviation = σ, then E(r) = d2(N)σ.
d3(N) is the standard deviation of the range of N observations from a normal population with σ = 1. Thus, if r is the range of a sample of N observations from a normal distribution with standard deviation = σ, then stdev(r) = d3(N)σ.
Use the following table to find an unbiasing constant for a given value, N. (To determine the value of N, consult the formula for the statistic of interest.)

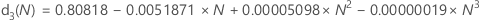
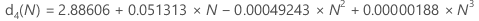
- D. J. Wheeler and D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
- H. Leon Harter (1960). "Tables of Range and Studentized Range". The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1.128 | 0.8525 | 0.954 |
| 3 | 1.693 | 0.8884 | 1.588 |
| 4 | 2.059 | 0.8798 | 1.978 |
| 5 | 2.326 | 0.8641 | 2.257 |
| 6 | 2.534 | 0.8480 | 2.472 |
| 7 | 2.704 | 0.8332 | 2.645 |
| 8 | 2.847 | 0.8198 | 2.791 |
| 9 | 2.970 | 0.8078 | 2.915 |
| 10 | 3.078 | 0.7971 | 3.024 |
| 11 | 3.173 | 0.7873 | 3.121 |
| 12 | 3.258 | 0.7785 | 3.207 |
| 13 | 3.336 | 0.7704 | 3.285 |
| 14 | 3.407 | 0.7630 | 3.356 |
| 15 | 3.472 | 0.7562 | 3.422 |
| 16 | 3.532 | 0.7499 | 3.482 |
| 17 | 3.588 | 0.7441 | 3.538 |
| 18 | 3.640 | 0.7386 | 3.591 |
| 19 | 3.689 | 0.7335 | 3.640 |
| 20 | 3.735 | 0.7287 | 3.686 |
| 21 | 3.778 | 0.7242 | 3.730 |
| 22 | 3.819 | 0.7199 | 3.771 |
| 23 | 3.858 | 0.7159 | 3.811 |
| 24 | 3.895 | 0.7121 | 3.847 |
| 25 | 3.931 | 0.7084 | 3.883 |
| N | d2(N) |
|---|---|
| 26 | 3.964 |
| 27 | 3.997 |
| 28 | 4.027 |
| 29 | 4.057 |
| 30 | 4.086 |
| 31 | 4.113 |
| 32 | 4.139 |
| 33 | 4.165 |
| 34 | 4.189 |
| 35 | 4.213 |
| 36 | 4.236 |
| 37 | 4.259 |
| 38 | 4.280 |
| 39 | 4.301 |
| 40 | 4.322 |
| 41 | 4.341 |
| 42 | 4.361 |
| 43 | 4.379 |
| 44 | 4.398 |
| 45 | 4.415 |
| 46 | 4.433 |
| 47 | 4.450 |
| 48 | 4.466 |
| 49 | 4.482 |
| 50 | 4.498 |
Unbiasing constants c4() and c5()
c4()

c5()

Notation
| Term | Description |
|---|---|
| Γ() | gamma function |
