Cette macro fournit les outils suivants pour effectuer une analyse spectrale : périodogramme, périodogramme cumulatif, fonction spectrale estimée et vérification du modèle spectral. Ces fonctions sont particulièrement utiles pour les procédés stationnaires et fournissent des méthodes d'analyse des effectifs pour les diagnostics de modèles ARIMA et de valeurs résiduelles.
Télécharger la macro
Assurez-vous que Minitab connaît l'emplacement de la macro que vous avez téléchargée. Sélectionnez . Sous Emplacement de la macro, accédez à l'emplacement où vous avez enregistré les fichiers macro.
Important
Si vous utilisez un ancien navigateur Web, lorsque vous cliquez sur le bouton Télécharger, il est possible que le fichier s'ouvre dans Quicktime, qui partage l'extension de fichier .mac avec les macros de Minitab. Pour enregistrer la macro, cliquez avec le bouton droit de la souris sur le bouton Télécharger, puis sélectionnez Enregistrer la cible sous.
Entrées requises
Vous avez besoin d'une colonne de données de série chronologique.
Entrées facultatives
- AR K…K
- Si vous disposez de paramètres autorégressifs estimés et que vous souhaitez effectuer une vérification du modèle spectral, saisissez ces paramètres ici.
- DIF K
- Si vous disposez d'une composante de calcul de différences, saisissez l'ordre de calcul des différences ici.
- MA K…K
- Si vous disposez de paramètres de moyenne mobile estimés et que vous souhaitez effectuer une vérification du modèle spectral, saisissez ces paramètres ici.
- VARIANCE K
- Saisissez votre variance estimée (valeur par défaut = 1,0).
- SMOOTH K
- Saisissez la longueur de la moyenne mobile (valeur par défaut = 3). La longueur de la moyenne mobile doit être un entier impair.
- ONEDOC
- Définissez ce paramètre si vous souhaitez que tous les graphiques apparaissent sur une page.
- SPERIOD C C
- Définissez ce paramètre si vous souhaitez stocker les coordonnées du périodogramme. La première colonne contiendra I(oméga) et la seconde colonne contiendra oméga.
- SCUMUL C C C C
- Définissez ce paramètre si vous souhaitez stocker les coordonnées du périodogramme cumulatif. La première colonne contiendra U(j), la deuxième contiendra la limite de signification supérieure, la troisième colonne contiendra la limite de signification inférieure et la quatrième colonne l'axe des X.
- SSPEC C C C C
- Définissez ce paramètre si vous souhaitez stocker les coordonnées pour l'estimation spectrale. La première colonne contiendra l'estimation spectrale, la deuxième colonne contiendra la limite de confiance supérieure, la troisième colonne contiendra la limite de confiance inférieure et la quatrième colonne contiendra oméga.
- SMODEL C C C C
- Définissez ce paramètre si vous souhaitez stocker les coordonnées pour la vérification du modèle spectral. La première colonne contiendra F(oméga), la deuxième contiendra la limite de confiance supérieure, la troisième contiendra la limite de confiance inférieure, la quatrième contiendra les estimations spectrales et la cinquième colonne contiendra oméga.
Exécution de la macro
Supposons que les données se trouvent en C1. Pour exécuter la macro, sélectionnez et saisissez :
%SPECTRAL C1Cliquez sur Essai.
Informations supplémentaires
Périodogramme
Le périodogramme est un outil qui peut être utilisé pour détecter des composantes cycliques dans une série chronologique. Le périodogramme est défini comme suit :
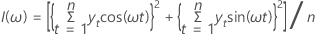
Lorsque le périodogramme est défini pour ω = 0, ce point est exclu car il correspond à la moyenne de l'échantillon (qui ne présente pas d'intérêt). Si n est impair, nous excluons ω = π.
Périodogramme cumulatif
Le périodogramme cumulatif est une application particulière du périodogramme permettant de tester l'hypothèse selon laquelle une série chronologique particulière constitue un bruit blanc gaussien. Le périodogramme cumulatif est un outil efficace pour le diagnostic des valeurs résiduelles. Le périodogramme cumulatif est défini comme suit :
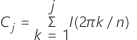
j = 1,...,m où m est le plus grand nombre entier strictement inférieur à n/2
Le diagramme de U j en fonction de j/(m −1) est appelé périodogramme cumulatif.
Nous pouvons également définir des valeurs critiques pour le test de l'hypothèse du bruit blanc gaussien. Le seuil de signification utilisé par la macro est de 10 % (valeur critique = 1,224). La région critique est définie par deux lignes parallèles ayant l'ordonnée à l'origine suivante :
Estimation spectrale
L'estimation spectrale,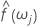 
, peut être dérivée simplement en prenant une moyenne mobile d'ordre 2p+1 (où p est un entier positif) des ordonnées calculées par le périodogramme. Nous pouvons également définir des limites de confiance à partir de cette estimation spectrale :
Les limites de confiance inférieure et supérieure peuvent être définies comme suit :
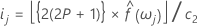
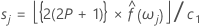
Spectre d'un procédé ARMA
L'estimation spectrale est l'estimation du spectre à partir des données. Le spectre est déterminé sur la base des valeurs réelles de la population pour les paramètres du modèle. Le spectre d'un procédé AR(p) peut être défini comme suit :
Le spectre d'un procédé MA(q) peut être défini comme suit :
Le spectre d'un procédé ARMA (p, q) (où p et q sont des ordres) peut être défini comme suit :
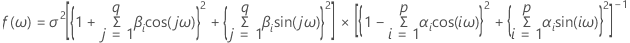
Vérification du modèle spectral pour un procédé ARIMA
Nous pouvons comparer l'estimation spectrale calculée à partir d'une série chronologique au spectre réel, en nous fondant sur les paramètres du modèle. De façon intuitive, si l'estimation spectrale est à peu près statistiquement égale au spectre réel, nous pouvons en conclure que les paramètres de notre modèle sont adaptés pour la modélisation de la série.
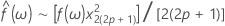
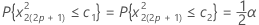
Ainsi, nous pouvons définir des limites de confiance pour déterminer si l'estimation du spectre se trouve dans ces limites.
Exemple 1
Pour voir un exemple du périodogramme, du périodogramme cumulatif et de l'estimation spectrale, consultez l'ensemble de données "Cycle 1, late follicular phase" (Diggle, p. 228). Pour exécuter la macro, sélectionnez et saisissez :
%SPECTRAL C1Pour commencer, le périodogramme (non affiché) indique que cette série présente une composante cyclique, à cause de son pic dominant. Une échelle plus significative est parfois adoptée pour l'axe des X, afin de vous permettre de déterminer plus facilement à quel moment la composante cyclique intervient. Pour cette raison, la macro comporte des options de stockage permettant à l'utilisateur de transformer l'axe (vous pouvez ensuite utiliser les fonctionnalités graphiques de Minitab pour générer des diagrammes). D'autre part, le périodogramme cumulatif indique que cette série ne constitue pas un bruit blanc gaussien, car certains des points de données se situent au-delà des limites de signification (représentées par les lignes parallèles en pointillés). Enfin, l'estimation spectrale (calculée par la moyenne mobile à 3 points) est représentée par la ligne rouge, tandis que les limites de confiance sont représentées par les lignes en pointillés. Ce diagramme nous aide à comprendre ce à quoi le spectre réel de la population peut ressembler. Ces trois diagrammes correspondent à ceux que l'on retrouve chez Diggle (p. 52, 55, 106).
Exemple 2
Pour une analyse ARIMA complète, reportez-vous à l'ensemble de données "Cycle 2, early follicular phase" (Diggle, p. 228). Calculez d'abord le périodogramme, le périodogramme cumulatif et l'estimation spectrale. Je placerai également ces trois diagrammes sur une page à l'aide de la sous-commande ONEDOC. Sélectionnez et saisissez :
%SPECTRAL C2;
ONEDOC.
Les graphiques (non affichés) indiquent clairement que cette série chronologique ne constitue pas un bruit blanc gaussien. En effet, le périodogramme et l'estimation spectrale montrent que nous sommes en présence d'une série à basse fréquence, comme le suggèrent les pics dominants constatés aux petites valeurs d'oméga et la présence de points significatifs dans le périodogramme cumulatif. Par conséquent, nous utiliserons MINITAB pour modéliser cette série à l'aide de l'algorithme ARIMA. Après avoir observé plusieurs modèles, nous en déduisons que le meilleur est un modèle AR(1).
Nous allons à présent utiliser la macro pour évaluer le modèle empirique. Soyez attentif à la façon dont l'estimation du paramètre autorégressif et l'estimation de la variance (à partir des résultats du modèle ARIMA) sont saisies dans le langage de commande suivante. Sélectionnez et saisissez :
%SPECTRAL C2;
AR 0.5860;
VARIANCE 0.20603;
ONEDOC.
Les diagrammes créés se contentent d'afficher à nouveau les graphiques rencontrés au cours de la vérification du modèle spectral. Dans le contexte de la vérification du modèle spectral, les cercles rouges représentent l'estimation spectrale et la ligne continue noire représente le spectre "réel", en fonction des paramètres estimés de notre modèle ARIMA. Les lignes en pointillés représentent les limites de confiance du spectre "réel". Etant donné que toutes les moyennes mobiles à 3 points (cercles rouges) sont comprises dans l'intervalle de confiance du spectre réel, nous pouvons conclure à la validité du modèle. Pour finir, nous devons exécuter la macro sur les valeurs résiduelles afin de nous assurer qu'elles sont le fait du bruit blanc gaussien. Le périodogramme cumulatif indique effectivement que ces valeurs résiduelles correspondent à un bruit blanc gaussien.
Références
Diggle, P. J. Time Series, A Biostatistical Introduction. Oxford: Clarendon Press, 1990.
