Télécharger la macro
Assurez-vous que Minitab connaît l'emplacement de la macro que vous avez téléchargée. Sélectionnez . Sous Emplacement de la macro, accédez à l'emplacement où vous avez enregistré les fichiers macro.
Important
Si vous utilisez un ancien navigateur Web, lorsque vous cliquez sur le bouton Télécharger, il est possible que le fichier s'ouvre dans Quicktime, qui partage l'extension de fichier .mac avec les macros de Minitab. Pour enregistrer la macro, cliquez avec le bouton droit de la souris sur le bouton Télécharger, puis sélectionnez Enregistrer la cible sous.
Entrées requises
Vous pouvez utiliser jusqu'à cinq matrices du plan.
Entrées facultatives
- MODEL (type de modèle)
- Indique le modèle à tester lors de l'exécution de l'expérience. Le type par défaut est Interaction. Vous pouvez saisir plusieurs modèles, tels que Linéaire, Quadratique, Interaction et Quadratique pur. Chaque modèle comprend les termes suivants :
- Linéaire : termes constants et linéaires
- Interaction : termes constants, linéaires et vectoriels
- Quadratique : interactions et termes carrés
- Quadratique pur : termes constants, linéaires et carrés
- RESOLUTION K
- Permet d'indiquer le nombre de points de plan échantillonnés pour estimer la variance de prévision minimale, maximale et intégrée à chaque valeur distincte du rayon. Pour les plans sujets à rotation, vous pouvez sélectionner une faible résolution. Pour les autres, vous devrez peut-être augmenter la résolution au fur et à mesure que le nombre de facteurs augmente. La valeur par défaut est de 500 points.
- INCREMENT K
- Permet d'indiquer la valeur d'incrémentation du rayon. Vous pouvez modifier cette valeur pour afficher le graphique avec une résolution plus élevée ou plus faible. La valeur par défaut est de 0,1 unité codée.
- MAXDIST K
- Indique la distance maximale du rayon. Par défaut, elle est définie comme la distance la plus grande au point le plus éloigné du centre du plan. Dans le cas d'un graphique de dispersion de la variance basé sur plusieurs plans, MAXDIST est la distance la plus grande de tous les plans.
Exécution de la macro
Supposons que les facteurs d'un CCD aient été copiés dans une matrice M1 et que les facteurs d'un plan de Box-Behnken soient stockés dans une matrice M2. Pour exécuter la macro, sélectionnez et saisissez :
%VDG M1 M2;
MODEL "quadratique";
RESOLUTION 150.Cliquez sur Essai.
Informations supplémentaires
Graphiques de dispersion de la variance et plan d'expériences
Les graphiques de dispersion de la variance sont des outils graphiques utilisés pour la sélection d'un plan d'expériences (DOE). Ces graphiques présentent la variance de prévision échelonnée d'un DOE dans l'espace de plan et sont généralement utilisés pour comparer les plans de surface de réponse. Toutefois, les graphiques de dispersion de la variance permettent également de comparer l'exécution de plusieurs plans pour un modèle spécifique, notamment un modèle linéaire, un modèle linéaire avec des termes d'interaction, un modèle linéaire avec des termes quadratiques ou un modèle quadratique complet.
Historique des graphiques de dispersion de la variance
A l'origine, le graphique de dispersion de la variance a été mis au point par Giovannitti-Jensen et Myers (1989) et Myers et al. (1992) pour présenter un aperçu de la stabilité de la variance de prévision échelonnée dans l'espace de plan.
Mathématiquement, la variance de prévision échelonnée peut être estimée à l'aide de l'équation suivante :
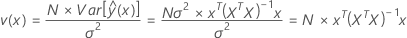
où v(x) est la variance de prévision échelonnée au point x qui, comme indiqué ci-dessus, ne dépend pas des données de réponse, mais uniquement de la matrice du plan X. En d'autres termes, la variance de prévision échelonnée est une fonction du nombre d'essais de votre expérience, de la matrice de covariance et du point auquel vous évaluez la variance de prévision. Comme la variance de prévision échelonnée présentée dans le graphique de dispersion de la variance ne dépend pas des données de réponse, le graphique vous aide à évaluer l'ajustement d'un plan a priori.
En général, un graphique de dispersion de la variance est créé à partir de quatre éléments de base :
- Un graphique de la variance sphérique en fonction du rayon r. La variance sphérique correspond à la valeur moyenne (intégrée) de v(x) à la surface d'une sphère de rayon r.
- · Un graphique de la variance de prévision maximale sur un rayon r pour plusieurs valeurs de r à partir de l'origine (r commence à zéro, puis augmente par petits incréments jusqu'à atteindre le point du plan le plus éloigné de l'origine).
- · Un graphique de la variance de prévision minimale sur un rayon r pour plusieurs valeurs de r à partir de l'origine.
- · Une ligne horizontale à v(x) = p, où p correspond au nombre de paramètres dans le modèle à ajuster. Dans un plan "optimal", la variance de prévision maximale est inférieure ou égale à p pour tous les points dans l'espace du plan.
Le graphique de dispersion de la variance affiche la variance de prévision échelonnée moyenne, maximale et minimale pour différentes valeurs de r, qui représente la distance de tout point par rapport à l'origine ou au centre du plan.
Utilisation d'un graphique de dispersion de la variance pour évaluer d'autres aspects d'un plan
Un graphique de dispersion de la variance vous permet d'évaluer l'exécution d'un seul plan en termes de variance de prévision. Vous pouvez également utiliser le graphique de dispersion de la variance pour comparer deux plans ou plus. Une autre application du graphique de dispersion de la variance consiste à évaluer l'effet de l'ajout de points centraux dans un plan.
Un graphique de dispersion de la variance permet de déterminer si un plan est sujet à rotation. Dans un plan sujet à rotation, les trois lignes (minimale, moyenne et maximale) dans le graphique coïncident toutes. Si ce n'est pas le cas, le plan centré de face n'est pas sujet à rotation.
Simulation de Monte-Carlo pour estimer la variance de prévision
Cette partie, destinée aux utilisateurs avancés, décrit les méthodes mathématiques utilisées pour estimer les variances de prévision minimale, maximale et moyenne affichées dans un graphique de dispersion de la variance. Si souhaitez seulement savoir comment exécuter la macro permettant d'afficher et d'interpréter un graphique de dispersion de la variance, vous pouvez passer à la partie suivante.
Comme indiqué précédemment, pour une valeur prédéterminée du rayon, des recherches doivent être effectuées pour trouver les variances de prévision échelonnées minimale, maximale et intégrée. La méthode sélectionnée pour la macro de Minitab repose sur la simulation de Monte-Carlo et la possibilité d'effectuer une recherche uniformément à des points situés à égale distance du centre x = (0,0,…,0)T du plan.
Trois quantités doivent être calculées à partir de distances différentes par rapport à l'origine : 1) la variance de prévision minimale, 2) la variance de prévision maximale et 3) la variance de prévision intégrée. Il existe plusieurs façons de connaître ces quantités. Une méthode possible consiste à utiliser un algorithme de programmation non linéaire permettant de connaître la variance de prévision minimale et maximale. Cependant, la méthode que nous avons choisie pour estimer ces quantités consiste à effectuer un échantillonnage uniforme et à trouver un grand nombre de points distincts se trouvant tous à la même distance du centre du plan pour différentes valeurs de r. En fonction de l'espace des points équidistants, l'estimation des variances de prévision minimale et maximale correcte est garantie par le respect de deux conditions. D'abord, l'échantillonnage des points équidistants doit être uniforme. C'est-à-dire qu'il ne peut pas y avoir de zones où certains points équidistants sont plus susceptibles d'être choisis que d'autres. Deuxièmement, le nombre de points doit être assez élevé pour pouvoir couvrir l'ensemble de l'espace des points de plan possibles.
Comme tous les points à échantillonner sont équidistants, réaliser cet échantillonnage revient à trouver une bonne méthode pour obtenir des points d'une n-boule ou d'une hypersphère pour un rayon donné.
La procédure est décrite dans l'ouvrage de Marsaglia (1972) et résumée ci-dessous :
- Générez un vecteur de dimension n de variables aléatoires normales (par exemple, à partir d'une loi normale standard). Le vecteur est défini comme suit : x = (x1, x2,…,xn). Créez plusieurs vecteurs x.
- Calculez le rayon ρ pour tous les points x générés.

- Transformez tous les points du plan d'origine obtenus à l'étape 1 en multipliant chaque entrée du vecteur x par r, où r représente le rayon de l'hypersphère utilisée pour l'échantillonnage.
Nous venons d'expliquer comment échantillonner des points dans une hypersphère de rayon r constant. Il est possible d'utiliser cette technique d'échantillonnage pour estimer la variance de prévision maximale ou minimale. A l'aide de ces échantillons et en tenant compte de la loi faible des grands nombres, la variance de prévision moyenne des points échantillonnés dans le plan peut être utilisée pour estimer la variance de prévision intégrée réelle si l'effectif n est suffisamment grand.
Références
[1] Marsaglia G. "Choosing a Point from the Surface of a Sphere". The Annals of Mathematical Statistics, Vol. 43, No. 2 (1972), pp. 645-646.
[2] Myers R, Montgomery D. (2002). (2002). Response Surface Methodology - Process and Product Optimization Using Designed Experiments, 2e édition. John Wiley & Sons, Inc.
