Un ingénieur qualité d’une usine de moteurs souhaite effectuer un test de bimodalité sur des pistons de deux fournisseurs. L’ingénieur mesure les longueurs d’un échantillon aléatoire de 100 pistons de chacun des fournisseurs.
Le script utilise le package diptest pour R afin de vérifier si les données sont unimodales. Si le test rejette l’hypothèse nulle pour les données unimodales, le script suppose que les données sont un mélange de deux distributions normales. Le script utilise le package mixtools pour R afin d’afficher des statistiques descriptives et des courbes de densité pour deux distributions normales.
- Transmettez une seule colonne d’une feuille de calcul Minitab en entrée.
- Ajoutez un titre de table.
- Ajouter des étiquettes de colonne pour une table.
- Envoyez une table dans le volet Sortie de Minitab.
- Créez un graphique et envoyez-le dans le volet Sortie Minitab.
| Fichier | Description |
|---|---|
| bimodal.R | Script R qui prend une colonne d’une feuille de calcul Minitab, teste l’unimodalité et produit des résultats pour une combinaison de deux distributions normales si les données ne sont pas unimodales. |
Tous les fichiers référencés dans ce guide sont disponibles dans ce fichier .ZIP : r_guide_files.zip.
Conditions préalables
-
Le script R dans l'exemple ci-dessous exige les packages R suivants :
- mtbr
- Package R qui intègre Minitab et R. Dans l'exemple, les fonctions de ce module envoient les résultats R à Minitab. Pour plus d’informations sur l’installation du package R de Minitab, passez à l’étape 2 : Installez mtbr.
- mixtools
- Le package R utilisé par le script pour créer une sortie pour un mélange de distributions normales.
- diptest
- Le package R utilisé par le script pour tester si les données sont unimodales.
install.packages("mixtools")Pour obtenir de l’aide sur l’installation des R packages, veuillez consulter le service d’assistance technique de votre organisation. L’assistance technique Minitab ne peut pas vous aider à installer des R packages.
Étapes d’exécution de l’exemple
- Vérifiez que vous avez installé les modules exigés : mtbr.
- Enregistrez le fichier de script R, bimodal.R, à votre emplacement de fichier par défaut Minitab. Pour plus d’informations sur l'emplacement où Minitab R recherche des fichiers de script, allez dans Dossiers par défaut pour les fichiers R pour Minitab.
- Ouvrez l’exemple de jeu de données CoûtEnergProcédé.MWX.
-
Dans le panneau Minitab Ligne de
commande, saisissez
RSCR "bimodal.R" "Process 1". - Sélectionnez Essai.
bimodal. R
# Load the necessary libraries
#Original code by Valentina Tillman
library(mixtools)
library(mtbr)
library(diptest)
# Retrieve sample data
input_column <- commandArgs(trailingOnly = TRUE)
data <- mtb_get_column(input_column)
dip_test_result <- dip.test(data)
if (dip_test_result$p.value < 0.05) {
# Fit a bimodal mixture model
bimodal_fit <- normalmixEM(data, k = 2)
# Manually extract parameter estimates and format them as a data frame
bimodal_table <- data.frame(
Mean = bimodal_fit$mu,
Standard_Deviation = bimodal_fit$sigma,
Proportion = bimodal_fit$lambda #tells you what % of the data is clustered around which mean. Also called lambda
)
# Define title and headers
mytitle <- "Modeling a Bimodal Distribution"
myheaders <- names(bimodal_table)
# Add the table to the mtbr output
mtb_add_table(columns = bimodal_table, headers = myheaders, title = mytitle)
png("r_bimodal_image.png")
plot(bimodal_fit, density = TRUE, which = 2)
graphics.off()
mtb_add_image("r_bimodal_image.png")
# Now generate tolerance intervals using the parameters found using mixtools
# Set the desired coverage level (e.g., 95%)
coverage_level <- 0.95
alpha <- 1 - coverage_level
# Calculate the tolerance intervals for each component
tolerance_intervals <- lapply(1:2, function(i) {
mu <- bimodal_fit$mu[i]
sigma <- bimodal_fit$sigma[i]
n <- bimodal_fit$lambda[i] # proportion of the component
# Calculate the critical value for the normal distribution
z <- qnorm(1 - alpha / (2 * n))
# Calculate lower and upper bounds of the tolerance interval
lower_bound <- mu - z * sigma
upper_bound <- mu + z * sigma
c(lower_bound, upper_bound)
})
# Show the tolerance intervals
tolerance_intervals_df <- data.frame(
Component = c("First Mode", "Second Mode"),
Lower_Bound = sapply(tolerance_intervals, "[", 1),
Upper_Bound = sapply(tolerance_intervals, "[", 2)
)
myheaders <- c("Component", "Lower Bound", "Upper Bound")
mytitle <- "Tolerance Intervals for Bimodal Distribution"
mtb_add_table(columns = tolerance_intervals_df, headers = myheaders, title = mytitle)
} else {
mtb_add_message("This data is unimodal.")
}
Résultats
Modeling a Bimodal Distribution
| Mean | Standard_Deviation | Proportion |
|---|---|---|
| 34.1875 | 1.50909 | 0.516129 |
| 48.3333 | 1.84992 | 0.483871 |
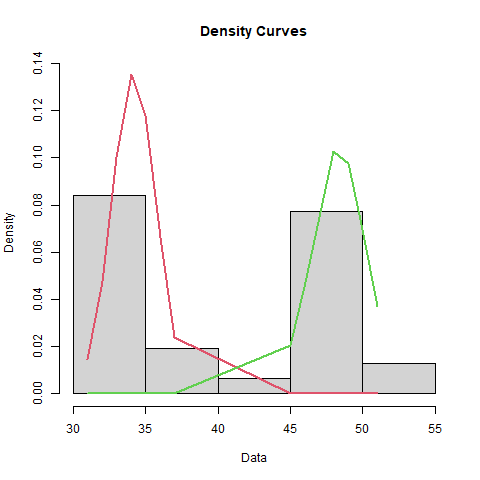
Tolerance Intervals for Bimodal Distribution
| Component | Lower Bound | Upper Bound |
|---|---|---|
| First Mode | 31.6821 | 36.6929 |
| Second Mode | 45.3200 | 51.3467 |
