Méthodes et formules pour le test des tableaux 2 x 2 pour la fonction Tableau à entrées multiples et Khi deux

Sélectionnez la méthode ou la formule de votre choix.

Sur ce thème

Test exact de Fisher
Test exact de McNemar
Test de Mantel-Haenszel-Cochran

Test exact de Fisher

Le test exact de Fisher est un test d'indépendance. Le test repose sur une loi exacte plutôt que sur une approximation de la loi du Khi deux utilisée pour les tests de Pearson et de rapport de vraisemblance. Le test exact de Fisher est utile lorsque les dénombrements de cellules attendus sont faibles et que l'approximation du Khi deux n'est pas très bonne.

Formule

La valeur de p est fondée sur une loi hypergéométrique avec les paramètres suivants :

effectif de la population: nombre total d'observations
nombre de réussites dans la population: nombre d'observations dans la première ligne
effectif de l'échantillon: nombre d'observations dans la première colonne

La valeur de p fournit une alternative bilatérale. Le calcul correspond à la somme des probabilités hypergéométriques pour les valeurs allant de 0 à l'effectif de la population qui sont inférieures ou égales à la probabilité de la valeur observée.

Exemple

Supposons que vous souhaitiez calculer la valeur de p pour le test exact de Fisher sur la préférence des cookies entre les adultes et les enfants.

	Enfant	Adulte	Total de la ligne
Au sucre	9	1	10
Aux pépites de chocolat	2	8	10
Total de la colonne	11	9	20

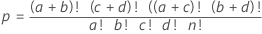
Fisher a montré que la probabilité d'obtenir cet ensemble de valeurs suit la loi hypergéométrique

qui se présente comme suit dans l'exemple :

	Enfant	Adulte	Total de la ligne
Au sucre	a	b	a+b
Aux pépites de chocolat	c	d	c+d
Total de la colonne	a+c	b+d	a+b+c+d

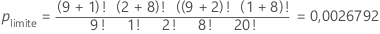
Dans le cas d'une matrice 2 x 2, vous pouvez calculer la valeur de p du test en additionnant toutes les valeurs de p inférieures à la probabilité conditionnelle de la matrice réelle. Ce calcule donne p_limite.

Pour cet exemple, la somme des valeurs de p inférieures ou égales à p_limite pour les autres matrices possibles est de 0,0054775.

Test exact de McNemar

Le test de McNemar compare les proportions observées avant et après un traitement. Vous pouvez par exemple l'utiliser pour déterminer si un programme de formation a un effet sur la proportion de participants qui répondent correctement à une question.

Les observations pour le test de McNemar peuvent être récapitulées dans un tableau 2 x 2, comme indiqué ci-dessous.

	Après traitement
Avant traitement	Condition Vraie	Condition Faux	Total
Condition Vraie	n ₁₁	n ₁₂	n_{1_.}
Condition Faux	n ₂₁	n ₂₂	n_{2_.}
Total	n_·1	n_·2	n_··

La condition pour l'exemple de la formation est une réponse correcte. Par conséquent, n₂₁ correspond au nombre de participants qui répondent correctement à la question après la formation, mais pas avant. En outre, n₁₂ représente le nombre de participants qui répondent correctement à la question avant la formation, mais pas après. Le nombre total de participants est représenté par n_...

Différence estimée

Soit δ la différence entre les probabilité marginales, p_1.- p_.1, dans la population. La différence estimée, , est obtenue par la formule suivante :

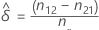
Intervalle de confiance

Un intervalle de confiance à 100(1 – α) % par approximation s'obtient par la formule suivante :

où α est le seuil de signification pour le test, z _α/2 est la valeur de Z associée à la probabilité aux extrémités de α/2, et l'erreur type s'obtient par la formule suivante :

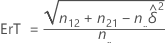
Valeur de p

L'hypothèse nulle est δ = 0. La valeur de p exacte pour le test de l'hypothèse nulle est calculée comme suit :

où X est une variable aléatoire issue d'une loi binomiale avec une probabilité d'événement de 0,5 et un nombre d'essais égal à n₂₁ + n₁₂.

Test de Mantel-Haenszel-Cochran

Le test suppose qu'aucune interaction à 3 facteurs n'existe. Le but de ce test est d'évaluer le degré d'association entre deux variables dichotomiques en tenant compte d'une variable de nuisance. La statistique de MHC est comparable à un percentile du Khi deux à un degré de liberté.

Le test de Mantel-Haenszel-Cochran (MHC) s'applique uniquement si au moins trois variables de classification existent et si les deux premières variables présentent deux niveaux chacune. Toutes les variables au-delà des deux premières sont traitées comme une variable Z unique dans le cadre du test MHC, où chaque combinaison de niveaux est traitée comme un niveau de Z.

Formule

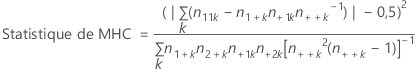
Notation

Terme	Description
k	niveau de Z
n_11k	nombre d'observations dans la première ligne, première colonne
n_1+k	nombre d'observations dans la première ligne
n_+1k	nombre d'observations dans la première colonne
n_++k	nombre total d'observations
n_2+k	nombre d'observations dans la seconde ligne
n_+2k	nombre d'observations dans la seconde colonne