Sur ce thème
Nombre de paires concordantes et discordantes
Une paire est concordante si l'observation étant élevée sur la variable X l'est également sur la variable Y. La paire est discordante si l'observation étant élevée sur X ne l'est pas sur Y. La paire est ex aequo si les sujets ont la même classification sur X et/ou sur Y.
Formule


Notation
| Terme | Description |
|---|---|
| nij | observations dans la cellule correspondant à la ie ligne et à la je colonne |
Gamma
Le gamma de Goodman et Kruskal permet de mesurer l'association entre des variables ordinales. Une association parfaite existe lorsque |γ| = 1. Si X et Y sont indépendants, γ = 0.
Formule

Notation
| Terme | Description |
|---|---|
| C | nombre de paires concordantes = Σi<kΣj<l nij nkl |
| D | nombre de paires discordantes = Σi<kΣj>l nij nkl |
| nij | observations dans la cellule correspondant à la ième ligne et à la jème colonne |
D de Somers
Le D de Somers mesure l'importance et la direction de la relation entre deux variables ordinales.
Formule
Y étant la variable de réponse :

X étant la variable de réponse :

Notation
| Terme | Description |
|---|---|
| TX | nombre de paires ex aequo sur X = 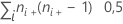 |
| TY | nombre de paires ex aequo sur Y = 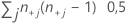 |
| C | nombre de paires concordantes |
| D | nombre de paires discordantes |
| ni+ | nombre d'observations dans la ième ligne |
| n+j | nombre d'observations dans la jème colonne |
| nij | observations dans la cellule correspondant à la ie ligne et à la je colonne |
| n++ | nombre total d'observations |
Tau b de Kendall
Le tau b de Kendall, comme gamma, mesure l'association entre des variables ordinales. L'un des avantages du tau b de Kendall en tant que mesure d'association est qu'il tient compte des paires ex aequo dans son calcul. Les paires ex aequo présentent un problème pour gamma, il indique donc presque toujours une association plus élevée que le tau b. Les valeurs du tau b sont comprises entre -1,0 et 1,0.
Formule

Notation
| Terme | Description |
|---|---|
| TX | nombre de paires ex aequo sur X = Σi ni+ (ni+- 1) 0,5 |
| TY | nombre de paires ex aequo sur Y = Σj n+j (n+j- 1) 0,5 |
| C | nombre de paires concordantes = Σi<kΣj<l nij nkl |
| D | nombre de paires discordantes = Σi<kΣj>l nij nkl |
| ni+ | nombre d'observations dans la ième ligne |
| n+j | nombre d'observations dans la jème colonne |
| nij | observations dans la cellule correspondant à la ième ligne et à la jème colonne |
| n++ | nombre total d'observations |
Test de concordance
Le test de concordance est un test d’indépendance. La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Formule
Le test de concordance utilise une statistique de test normale standard :

La valeur de p est égale à la probabilité que Z soit supérieur à Z*.
Notation
| Terme | Description |
|---|---|
| C | nombre de paires concordantes = Σi<kΣj<l nij nkl |
| D | nombre de paires discordantes = Σi<kΣj>l nij nkl |
| SE (C-D) | Erreur type ou C-D, qui est approximativement égale à 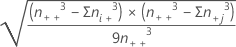 |
| n++ | nombre total d'observations |
| ni+ | le nombre d’observations dans la ième ligne. |
| n+j | Le nombre d’observations dans la jème colonne. |
