Sélectionnez la méthode ou la formule de votre choix.
Sur ce thème
Valeur attendue pour chaque catégorie
Formule
La valeur attendue, E, pour chaque catégorie, i, est calculée comme suit :
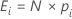
Notation
| Terme | Description |
|---|---|
| pi | proportion de test pour la ie catégorie, ce qui correspond à 1/k ou à la valeur fournie |
| k | nombre de catégories distinctes |
| N | nombre total de valeurs observées (O1 + ... + Ok) |
| Oi | valeur observée pour la ie catégorie |
Statistique du test du Khi deux
Formule
La statistique du test du Khi deux est calculée de la façon suivante :
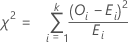
Notation
| Terme | Description |
|---|---|
| k | nombre de catégories distinctes |
| Oi | valeur observée pour la ie catégorie |
| Ei | valeur attendue pour la ie catégorie |
Contribution à la statistique du Khi deux
Formule
La contribution de la ie catégorie à la valeur du Khi deux est la suivante :

Notation
| Terme | Description |
|---|---|
| Oi | valeur observée pour la ie catégorie |
| Ei | valeur attendue pour la ie catégorie |
Degrés de liberté (DL)
Formule
Les degrés de liberté (DL) sont calculés comme suit :

Notation
| Terme | Description |
|---|---|
| DL | degrés de liberté |
| k | nombre de catégories |
Valeur de p
Formule
La valeur de p se calcule comme suit : Prob (Χ > statistique de test)
Notation
| Terme | Description |
|---|---|
| X | suit une loi du Khi deux avec k – 1 degrés de liberté |
Exemple de calcul
Soit :
| Catégorie i | Oi observé | Proportion testée : pi |
|---|---|---|
| A | 5 | 0,1 |
| B | 15 | 0,2 |
| C | 10 | 0,3 |
| D | 10 | 0,4 |
| N=40 |
Calculé :
| Catégorie i | Valeur attendue
Ei = (pi * N) |
Contribution au Khi deux
(Oi- Ei)2 / Ei |
|---|---|---|
| A | 0,1 * 40 = 4 | (5 – 4)2 / 4 = 0,25 |
| B | 0,2 * 40 = 8 | (15 – 8)2 / 8 = 6,125 |
| C | 0,3 * 40 = 12 | (10 – 12)2 / 12 = 0,3333 |
| D | 0,4 * 40 = 16 | (10 – 16)2 / 16 = 2,25 |
χ2 = 0,2500 + 6,1250 + 2,2500 + 0,3333 = 8,9583
DF = k – 1 = 3
valeur de p = Prob (Χ > 8,9583) = 0,0299
Notation
| Terme | Description |
|---|---|
| DL | degrés de liberté |
| k | nombre de catégories |
