Interprétation de toutes les statistiques et de tous les graphiques pour la fonction Test d'ajustement du Khi deux

Obtenez des définitions et bénéficiez de conseils en matière d'interprétation pour toutes les statistiques et tous les graphiques fournis avec le test d'ajustement du Khi deux.

Sur ce thème

Carte des contributions à la valeur du Khi deux
Carte des valeurs observées et attendues
Khi deux et contribution au Khi deux
DL

N
Valeurs observées et attendues
Valeur de p

Carte des contributions à la valeur du Khi deux

Ce diagramme à barres détermine la contribution des catégories à la statistique totale de Khi deux. Vous pouvez choisir un tableau classant les catégories par contribution, de la plus importante à la plus petite.

Interprétation

Les catégories dont la différence entre la valeur observée et la valeur attendue est importante apportent une plus importante contribution à la statistique de Khi deux.

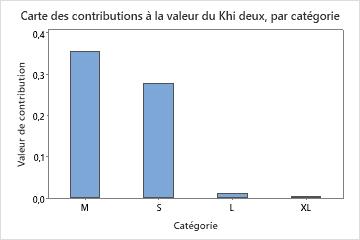
Cette carte barre indique que la contribution à la statistique du Khi deux la plus importante se trouve dans la catégorie M.

Carte des valeurs observées et attendues

Utilisez une carte barre représentant les valeurs observées et attendues pour chaque catégorie afin de déterminer si une catégorie spécifique présente une différence.

Si vous avez déterminé que la différence entre les dénombrements observés et attendus est statistiquement significative, vous pouvez utiliser cette carte barre pour déterminer les catégories pour lesquelles la différence entre valeurs observées et attendues est la plus grande.

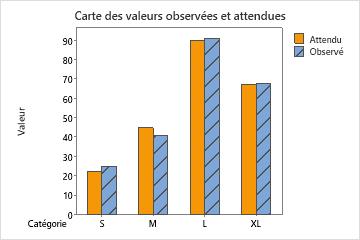
Cette carte barre indique que les valeurs observées sont très proches des valeurs attendues pour chaque catégorie. Ainsi, la carte barre confirme visuellement que la valeur de p indique qu'il n'est pas possible de conclure que les proportions observées sont significativement différentes des proportions indiquées.

Khi deux et contribution au Khi deux

Utilisez les contributions individuelles par catégorie pour quantifier la quantité du total des statistiques de Khi deux imputable à la différence de chaque catégorie entre les valeurs observées et celles attendues.

Minitab calcule la contribution de chaque catégorie à la statistique de Khi deux comme le carré de la différence entre les valeurs observées et attendues d'une catégorie, divisé par la valeur attendue de cette dernière. La statistique du Khi deux est la somme de ces valeurs pour toutes les catégories.

Interprétation

Les catégories dont la différence entre la valeur observée et la valeur attendue est importante apportent une plus importante contribution à la statistique de Khi deux.

Dans ces résultats, les valeurs de contribution de chaque catégorie s'ajoutent à la statistique totale de Khi deux, qui est de 0,648. La contribution la plus importante provient des tee-shirts de taille M et la plus petite provient de la catégorie XL.

DL

Le nombre de degrés de liberté du test d'ajustement du Khi deux correspond au nombre de catégories moins 1.

Interprétation

Minitab utilise les degrés de liberté pour déterminer la valeur de p. Plus votre étude compte de catégories, plus il y a de degrés de liberté.

Dans ces résultats, le nombre de degrés de liberté (DL) est de 3.

Test du Khi deux

N	DL	Khi deux	Valeur de P
225	3	0,648148	0,885

N

N représente l'effectif total de l'échantillon. N est égal à la somme de tous les dénombrements observés.

Interprétation

Dans ces résultats, l'effectif total de l'échantillon (N) est 225.

Dénombrements observés et attendus

Catégorie	Observé	Proportion testée	Attendu	Contribution au Khi deux
S	25	0,1	22,5	0,277778
M	41	0,2	45,0	0,355556
L	91	0,4	90,0	0,011111
XL	68	0,3	67,5	0,003704

Test du Khi deux

N	DL	Khi deux	Valeur de P
225	3	0,648148	0,885

Valeurs observées et attendues

Les valeurs observées sont le nombre réel d'observations dans un échantillon qui appartiennent à une catégorie.

Les valeurs attendues correspondent au nombre d'observations estimé en moyenne, si les proportions du test étaient vraies. Minitab calcule les valeurs attendues en multipliant les proportions de test de chaque catégorie par l'effectif total de l'échantillon.

Interprétation

Vous pouvez comparer les valeurs observées et attendues en utilisant le tableau de résultats ou le diagramme à bâtons.

Dans ces résultats, les dénombrements attendus ne semblent pas très proches des dénombrements observés pour toutes les catégories.

Valeur de p

La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.

Utilisez la valeur de p pour déterminer si l'hypothèse nulle doit être rejetée ou non, hypothèse supposant que les proportions de population de chaque catégorie sont cohérentes avec les valeurs indiquées dans chaque catégorie.

Interprétation

Pour déterminer si les valeurs observées dans l'échantillon et les valeurs attendues de la loi spécifiée sont statistiquement différentes, comparez la valeur de p au seuil de signification. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de rejeter à tort l'hypothèse nulle.

Valeur de p ≤ α : les données observées sont statistiquement différentes des valeurs attendues (rejeter H₀): Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et en conclure que vos données ne suivent pas une loi avec certaines proportions. Utilisez vos connaissances afin de déterminer si la différence est significative dans la pratique.
Valeur de p > α : vous ne pouvez pas conclure que les données observées sont statistiquement différentes des valeurs attendues (ne pas rejeter H₀): Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle, car vous n'êtes pas en mesure de conclure que les données ne suivent pas la loi avec des proportions spécifiées. Toutefois, vous ne pouvez pas conclure que les lois sont identiques. S'il est possible qu'il existe une différence, votre test peut ne pas être suffisamment puissant pour la détecter.

Dans ces résultats, la valeur de p est 0,885. Comme la valeur de p est supérieure à la valeur α choisie de 0,05, vous ne pouvez pas rejeter l'hypothèse nulle. Vous ne pouvez donc pas conclure que les proportions observées sont significativement différentes des proportions indiquées.

Test du Khi deux

N	DL	Khi deux	Valeur de P
225	3	0,648148	0,885