Sur ce thème
Moyenne (normale)
L'écart type est connu
L'intervalle de confiance pour une moyenne à partir d'une loi normale lorsque l'écart type de la population est connu est :

La marge d'erreur est de 
Pour résoudre n :

L'écart type est inconnu
L'intervalle de confiance pour une moyenne à partir d'une loi normale lorsque l'écart type de la population est inconnu est :
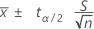
La marge d'erreur est de 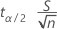
Pour résoudre n, calculez la valeur minimale de n comme suit :
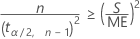
Notation
| Terme | Description |
|---|---|
 | moyenne de l'échantillon |
| zα/2 | probabilité cumulée inverse de la loi normale standard à 1- α /2 ; α = 1 - niveau de confiance/100 |
| σ | écart type d'une population (supposé connu) |
| n | effectif d'échantillon |
| ME | marge d'erreur |
| t α/2 | probabilité cumulée inverse d'une loi T avec n-1 degrés de liberté à 1-α/2 |
| S | valeur prévisionnelle |
Proportion (binomiale)
Limite inférieure
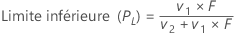
Limite supérieure

L'intervalle (PL, PU) est un intervalle de confiance approximatif à 100(1 – α) % de p.
Remarque
Pour résoudre n, calculez la valeur minimale de n comme suit :
Notation
| Terme | Description |
|---|---|
| v1 (limite inférieure) | 2x |
| v2 (limite inférieure) | 2(n – x + 1) |
| v1 (limite supérieure) | 2(x + 1) |
| v2 (limite supérieure) | 2(n – x) |
| x | nombre d'événements |
| n | Nombre de répliques |
| F (limite inférieure) | point inférieur α/2 de la loi F avec v1 et v2 degrés de liberté |
| F (limite supérieure) | point supérieur α/2 de la loi F avec v1 et v2 degrés de liberté |
Taux et moyenne (Poisson)
Formule
La limite de confiance de borne inférieure pour un taux ou une moyenne d'une loi de Poisson est :
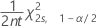
La limite de confiance de borne supérieure pour un taux ou une moyenne d'une loi de Poisson est :
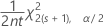
La marge d'erreur inférieure est égale à −1 × (limite de confiance de borne inférieure). La marge d'erreur supérieure est égale à la limite de confiance de borne supérieure.
Pour résoudre n, calculez la valeur minimale de n comme suit :
(S – SL) ≤ ME et (SU – S) ≤ ME
Notation
| Terme | Description |
|---|---|
| n | effectif d'échantillon |
| t | longueur d'observation ; pour la moyenne de Poisson, longueur = 1 |
| s | nombre total d'occurrences dans un procédé de Poisson |
| χ2p, x | point de percentile supérieur x d'une loi du Khi deux avec p degrés de liberté, où 0 < x < 1 |
| S | valeur prévisionnelle |
| ME | marge d'erreur |
Variance et écart type (normal)
Formule
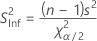
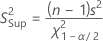
Pour obtenir l'intervalle de confiance de l'écart type, utilisez la racine carrée des équations ci-dessus.
La marge d'erreur inférieure est égale à −1 × (limite de confiance de borne inférieure). La marge d'erreur supérieure est égale à la limite de confiance de borne supérieure.
Pour résoudre n pour la variance, calculez la valeur minimale de n comme suit :
(S2 – S2L) ≤ ME et (S2U – S2) ≤ ME
Pour résoudre n pour l'écart type, calculez la valeur minimale de n comme suit :
(S – SL) ≤ ME et (SU – S) ≤ ME
Notation
| Terme | Description |
|---|---|
| n | effectif d'échantillon |
| s2 | variance d'échantillon |
| Χ2 p | 100pème point de percentile supérieur sur une loi du Khi deux avec (n – 1) degrés de liberté |
| S | valeur prévisionnelle |
| ME | marge d'erreur |
