Sur ce thème
Paramètre
Le paramètre affiche la statistique que vous avez sélectionnée dans la boîte de dialogue. Les paramètres sont des mesures descriptives de la totalité d'une population utilisées en tant qu'entrées d'une fonction de loi de probabilité (PDF) pour générer des courbes de distribution. Pour plus d'informations, reportez-vous à la rubrique Que sont les paramètres, estimations de paramètres et lois d'échantillonnage ?
Longueur d'observation
Les procédés de Poisson comptent les occurrences d'un certain événement ou propriété sur une plage d'observations spécifique, pouvant représenter notamment la période, la région, le volume et le nombre d'éléments. La longueur d'observation représente l'ampleur, la longueur ou la taille de chaque plage d'observations.
Interprétation
Minitab utilise la longueur d'observation pour exprimer le taux d'occurrence de la façon la mieux adaptée à votre situation.
Par exemple, si chaque observation d'un échantillon compte le nombre d'événements survenant dans une année, une longueur de 1 représente un taux d'occurrence annuel, alors qu'une longueur de 12 représente un taux d'occurrence mensuel.
- Le nombre total d'occurrences est de 122 car les inspecteurs ont relevé 122 défauts.
- L'effectif de l'échantillon (N) est de 50 car les inspecteurs ont échantillonné 50 paquets.
- Pour déterminer le nombre de défauts par serviette, les inspecteurs utilisent une longueur d'observation de 10 car chaque paquet contient 10 serviettes. Pour déterminer le nombre de défauts par paquet, les inspecteurs utilisent une longueur d'observation de 1.
- Le taux d'occurrence est égal à : (nombre total d'occurrences/N) / (longueur d'observation) = (122/50) / 10 = 0,244. Ainsi, chaque serviette comporte 0,244 défaut en moyenne.
Loi de distribution
- Normale
-
La loi normale standard est une loi en forme de cloche dans laquelle les écarts types successifs par rapport à la moyenne fournissent des références pour l'estimation du pourcentage des observations de données. Ces références sont à la base d'un grand nombre de tests d'hypothèse, tels que les tests Z et les tests t.
Par exemple, la taille de tous les hommes adultes qui résident dans l'état de Pennsylvanie, aux Etats-Unis, est à peu près normalement distribuée. La taille de la plupart des hommes avoisine par conséquent la taille moyenne (1,75 m). Un nombre similaire d'hommes mesure un peu plus ou un peu moins de 1,75 m. Seuls quelques-uns sont beaucoup plus grands ou beaucoup plus petits que la moyenne.
- Binomiale
-
Lorsque vous classez indépendamment des éléments, des événements ou des personnes en deux catégories, le nombre d'éléments, d'événements ou de personnes dans une catégorie suit une loi binomiale. Les deux catégories doivent être strictement exclusives, par exemple, oui/non, succès/échec ou défectueux/non défectueux.
Par exemple, des ingénieurs examinent un échantillon de boulons afin de déterminer s'ils présentent d'importantes fissures, susceptibles de les rendre inutilisables. Les boulons ne présentant pas de fissures ne sont pas défectueux et ceux qui en présentent sont défectueux.
- Poisson
-
Lorsque vous dénombrez la présence d'une caractéristique, d'un résultat ou d'une activité sur une certaine durée, un certain domaine ou une autre étendue d'observation, vous obtenez des données de Poisson. Les données de Poisson sont évaluées en dénombrements par unité, chaque unité ayant le même effectif.
Par exemple, les inspecteurs d'une société de transport en commun calculent le nombre de pannes de bus chaque jour pendant 30 jours.
Ecart type
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données par rapport à la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit. La valeur affichée par Minitab est la valeur prévisionnelle indiquée dans la boîte de dialogue.
Proportion
Une proportion est une part relative d'un ensemble, par opposition à un dénombrement ou à une fréquence. La proportion est égale au nombre d'événements divisé par l'effectif de l'échantillon. La valeur affichée par Minitab est la valeur prévisionnelle indiquée dans la boîte de dialogue.
Evaluation
Le taux d'occurrence d'un événement est le nombre moyen d'occurrences de cet événement par longueur d'observation. La valeur affichée par Minitab est la valeur prévisionnelle indiquée dans la boîte de dialogue.
Moyenne
Une moyenne de Poisson représente le nombre moyen d'occurrences d'un événement dans la totalité de l'espace d'observation. La valeur affichée par Minitab est la valeur prévisionnelle indiquée dans la boîte de dialogue.
Niveau de confiance
Un niveau de confiance à 95 % est généralement efficace. Il indique que 19 échantillons sur 20 (95 %) d'une même population génèrent des intervalles de confiance qui contiennent le paramètre de population.
Le niveau de confiance représente le pourcentage d'intervalles qui incluraient le paramètre de population si vous utilisiez plusieurs fois des échantillons de la même population. Par conséquent, si vous collectez 100 échantillons et que vous faites 100 intervalles de confiance à 95 %, vous vous attendriez à ce qu'environ 95 intervalles contiennent le paramètre de population, tel que la moyenne de la population, comme l'illustre la figure suivante.
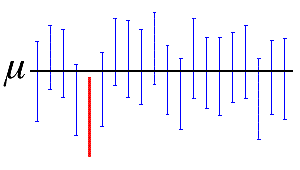
Dans cette figure, la ligne horizontale représente la valeur fixe de la moyenne de population inconnue, µ. Les 19 intervalles de confiance bleus verticaux qui chevauchent la ligne horizontale comprennent la valeur de la moyenne de population. Ce qui n'est pas le cas de l'intervalle de confiance rouge situé complètement en dessous de la ligne horizontale.
Intervalle de confiance
Minitab affiche le type d'intervalle de confiance indiqué dans la boîte de dialogue.
L'intervalle de confiance fournit une étendue de valeurs probables pour la proportion de la population. Les échantillons étant aléatoires, il est peu probable que deux échantillons d'une population donnent des intervalles de confiance identiques. Toutefois, si vous répétiez l'échantillonnage de nombreuses fois, un certain pourcentage des intervalles de confiance ou bornes obtenus contiendrait le paramètre de population inconnu. Le pourcentage de ces intervalles de confiance ou bornes contenant le paramètre est le niveau de confiance de l'intervalle.
Une borne supérieure définit une valeur à laquelle le paramètre de population est susceptible d'être inférieur. Une borne inférieure définit une valeur à laquelle le paramètre de population est susceptible d'être supérieur.
