Sur ce thème
Seuil de signification (α)
Le niveau de signification (dénoté par alpha ou α) est le niveau maximal acceptable du risque de commettre une erreur de type I.
Interprétation
Le seuil de signification permet de décider si un effet est significatif sur le plan statistique. Etant donné que le seuil de signification est le seuil de la signification statistique, une valeur plus élevée augmente les risques de commettre une erreur de type I. Une erreur de type I consiste à conclure à tort qu'un effet est significatif sur le plan statistique.
Ecart type supposé
L'écart type supposé correspond à l'estimation de l'écart type des mesures de réponses prises durant les essais expérimentaux répétés. Si vous avez déjà effectué dans Minitab une analyse ayant produit un tableau ANOVA, vous pouvez utiliser la racine carrée du carré de la moyenne ajustée pour l'erreur.
Interprétation
Utilisez l'écart type supposé pour décrire la variabilité des données. Des valeurs plus élevées de l'écart type supposé indiquent une plus grande variation, ou "bruit", dans les données, ce qui diminue la puissance statistique d'un plan.
Facteurs
Le nombre indique combien de facteurs sont présents dans le plan.
Interprétation
Utilisez le nombre de facteurs pour vérifier que le plan comporte tous les facteurs à étudier. Les facteurs sont les variables que vous contrôlez dans l'expérience. Ils sont également appelés variables indépendantes, variables explicatives ou variables de prédiction. Pour les calculs de la puissance et de l'effectif de l'échantillon, tous les facteurs sont numériques. Les facteurs numériques utilisent quelques valeurs contrôlées dans l'expérience, même si de nombreuses valeurs sont possibles. Ces valeurs sont appelées niveaux de facteurs.
Par exemple, vous étudiez les facteurs susceptibles d'avoir un impact sur la résistance du plastique durant le processus de fabrication. Vous décidez d'inclure Température dans votre expérience. Etant donné que la température est un facteur, seuls trois paramètres de températures sont dans l'expérience : 100 °C, 150 °C et 200 °C.
Style
Le nombre indique combien de sommets sont présents dans une répétition.
Interprétation
Ce nombre permet d'identifier le plan de Plackett-Burman utilisé par les calculs de puissance. Un sommet est un essai expérimental où les facteurs sont à leurs niveaux élevés ou faibles.
Points centraux
Le nombre indique combien de points centraux sont dans le plan.
Interprétation
Utilisez le nombre de points centraux pour voir l'effet des différents nombres de points centraux sur les résultats. Les points centraux représentent les essais où tous les facteurs sont définis à mi‑chemin entre les niveaux minimaux et maximaux.
Les points centraux ont en général une petite influence sur les résultats lorsque le plan inclut des répétitions des sommets. Outre leur influence sur les calculs des puissances, ils peuvent être utilisés à d'autres fins. Par exemple, le test de courbure dans la réponse nécessite des points centraux.
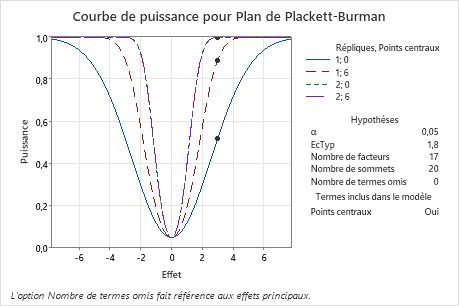
Dans ces résultats, les points sur les courbes de puissance indiquent les calculs pour une différence de 3. Le plan avec 1 répétition et aucun point central présente une puissance proche de 0,5. Le plan avec 1 répétition et 6 points centraux présente une puissance de quasiment 0,9. Avec deux répétitions, les courbes de puissance pour 0 point central et 6 points centraux sont indistinguables sur le graphique. La courbe pour 6 points centraux est légèrement supérieure pour les effets différents de zéro. Les valeurs de puissance sont toutes deux proches de 1.
Méthode
| Facteurs : | 17 | Plan : | 20 |
|---|
Résultats
| Points centraux | Effet | Répliques | Nombre total d'essais | Puissance |
|---|---|---|---|---|
| 0 | 3 | 1 | 20 | 0,517308 |
| 0 | 3 | 2 | 40 | 0,998927 |
| 6 | 3 | 1 | 26 | 0,889603 |
| 6 | 3 | 2 | 46 | 0,999082 |
Effet
Si vous entrez le nombre de répétitions, la valeur de puissance et le nombre de points centraux, Minitab calcule l'effet. L'effet est la différence dans la réponse entre les niveaux supérieur et inférieur d'un facteur, que le plan doit détecter. Cette différence est le résultat d'un facteur isolé (effet principal).
Interprétation
Utilisez l'effectif de l'échantillon pour déterminer la capacité du plan à détecter un effet. Si vous entrez un nombre de répétitions, une puissance et un nombre de points centraux, Minitab calcule le plus petit effectif d'échantillon que le plan peut détecter avec la puissance indiquée. En général, un grand nombre de répétitions permet à une expérience conçue de détecter de plus petits effets.
Dans ces résultats, le plan avec une répétition peut détecter une différence d'environ 0,015 avec une puissance de 80 %. La différence que le plan peut détecter avec une puissance de 90 % est d'environ 0,018 ; elle est donc supérieure à 0,015. Le plan avec 2 répétitions peut détecter avec une puissance de 80 % une différence d'environ 0,007 ; elle est donc inférieure à 0,015.
Méthode
| Facteurs : | 31 | Plan : | 32 |
|---|---|---|---|
| Points centraux (total) : | 4 |
Résultats
| Points centraux | Répliques | Nombre total d'essais | Puissance | Effet |
|---|---|---|---|---|
| 4 | 1 | 36 | 0,8 | 0,0153027 |
| 4 | 1 | 36 | 0,9 | 0,0180278 |
| 4 | 2 | 68 | 0,8 | 0,0073261 |
| 4 | 2 | 68 | 0,9 | 0,0084775 |
Répliques
On parle de répétitions lorsque plusieurs essais expérimentaux sont effectués avec les mêmes paramètres de facteurs.
Interprétation
Utilisez le nombre de répétitions pour déterminer le nombre d'essais expérimentaux à inclure dans le plan. Si vous entrez une puissance, l'effectif d'échantillon et le nombre de points centraux, Minitab calcule le nombre de répétitions. Etant donné que les nombres de répétitions et de points centraux sont des valeurs entières, la puissance réelle peut être supérieure à votre valeur cible. L'augmentation du nombre de répétitions augmente également la puissance du plan. Le nombre de répétitions doit être suffisant pour atteindre la puissance adéquate.
Etant donné que les répétitions sont des valeurs entières, les valeurs de puissance indiquées sont les valeurs de puissance cible. Les valeurs de puissance réelles sont pour le nombre de répétitions et le nombre de points centraux dans l'expérience conçue. Elles sont supérieures ou égales aux valeurs de puissance cible.
Dans ces résultats, Minitab calcule le nombre de répétitions nécessaires pour atteindre la puissance cible. Le plan qui détecte un effet de 2 avec une puissance de 0,8 nécessite 1 répétition. Pour atteindre une puissance de 0,9, le plan nécessite 2 répétitions. La puissance réelle avec 2 répétitions est supérieure à 0,99. Il s'agit de la plus petite valeur de puissance supérieure ou égale à 0,9 et elle peut être obtenue en utilisant un nombre entier de répétitions. Pour détecter le plus petit effet de 0,9 avec une puissance de 0,8, le plan nécessite 4 répétitions. Pour détecter le plus petit effet de 0,9 avec une puissance de 0,9, le plan nécessite 5 répétitions.
Méthode
| Facteurs : | 15 | Plan : | 32 |
|---|---|---|---|
| Points centraux (total) : | 0 |
Résultats
| Points centraux | Effet | Répliques | Nombre total d'essais | Puissance cible | Puissance réelle |
|---|---|---|---|---|---|
| 0 | 2,0 | 1 | 32 | 0,8 | 0,877445 |
| 0 | 2,0 | 2 | 64 | 0,9 | 0,995974 |
| 0 | 0,9 | 4 | 128 | 0,8 | 0,843529 |
| 0 | 0,9 | 5 | 160 | 0,9 | 0,914018 |
Nombre total d'essais
Un essai expérimental est une combinaison de niveaux de facteurs à laquelle vous mesurez les réponses. Le nombre total d'essais représente le nombre de mesures de la réponse contenues dans le plan. De multiples exécutions de la même combinaison de niveaux de facteurs sont considérées comme des essais distincts et sont appelées répétitions.
Interprétation
Utilisez le nombre total d'essais pour vérifier que la taille de l'expérience conçue est adaptée pour vos ressources. Pour un plan de Plackett-Burman, cette formule permet d'obtenir le nombre total d'essais :

| Terme | Description |
|---|---|
| n | Nombre de sommets par répétition |
| r | Nombre de répliques |
| cptotal | Nombre de points centraux |
Dans ces résultats, un plan avec 12 sommets et 4 points centraux compte au total 16 essais. Le nombre d'essais dans 2 répétitions du plan est 12*2 + 4 = 28.
Méthode
| Facteurs : | 8 | Plan : | 12 |
|---|---|---|---|
| Points centraux (total) : | 4 |
Résultats
| Points centraux | Effet | Répliques | Nombre total d'essais | Puissance |
|---|---|---|---|---|
| 4 | 2,5 | 1 | 16 | 0,523009 |
| 4 | 2,5 | 2 | 28 | 0,895399 |
Puissance
La puissance d'un plan est la probabilité selon laquelle le plan détermine qu'un effet est significatif sur le plan statistique. La différence entre les moyennes de la variable de réponse aux niveaux supérieur et inférieur d'un facteur est l'effectif de l'échantillon.
Interprétation
Utilisez la valeur de puissance pour déterminer la capacité du plan à détecter une différence. Si vous entrez une puissance, l'effectif d'échantillon et le nombre de points centraux, Minitab calcule le nombre de répétitions. La valeur de puissance 0,9 est généralement appropriée. Une valeur de 0,9 indique que vous avez 90 % de chances de détecter un effet. En général, lorsque le nombre de répétitions est plus petit, la puissance est inférieure. Si un test a une faible puissance, vous pouvez ne pas réussir à détecter un effet et conclure à tort qu'aucun effet n'existe.
Ces résultats montrent comment une augmentation du nombre d'essais augmente la puissance. Pour un effet de 0,9, la puissance du plan est d'environ 0,55 avec 64 essais au total. Avec un total de 160 essais, la puissance du plan passe à environ 0,91.
En outre, ces résultats montrent comment une augmentation de l'importance de l'effet augmente également la puissance. Pour un plan à 64 essais, la puissance est d'environ 0,55 pour un effet de 0,9. Avec une importance de l'effet de 1,5, la puissance du plan augmente et passe à environ 0,93.
Méthode
| Facteurs : | 15 | Plan : | 32 |
|---|---|---|---|
| Points centraux (total) : | 0 |
Résultats
| Points centraux | Effet | Répliques | Nombre total d'essais | Puissance |
|---|---|---|---|---|
| 0 | 1,5 | 5 | 160 | 0,999830 |
| 0 | 1,5 | 2 | 64 | 0,932932 |
| 0 | 0,9 | 5 | 160 | 0,914018 |
| 0 | 0,9 | 2 | 64 | 0,545887 |
Courbe de la puissance
La courbe de puissance trace la puissance du plan en fonction de l'importance de l'effet. Un effet est la différence de la valeur de réponse moyenne aux niveaux maximum et minimum d'un facteur.
Interprétation
La courbe de puissance vous permet d'évaluer les propriétés adaptées pour le plan.
La courbe de puissance représente la relation entre la puissance et l'effectif de l'échantillon pour toutes les combinaisons de points centraux et de répétitions. Chaque symbole sur la courbe de puissance représente une valeur calculée en fonction des propriétés saisies. Par exemple, si vous entrez un nombre de répétitions, une valeur de puissance et un nombre de points centraux, Minitab calcule l'importance correspondante de l'effet et affiche la valeur calculée sur le graphique pour la combinaison de répétitions et de points centraux. Pour la résolution des répétitions ou des points centraux, le diagramme inclut également les courbes d'autres combinaisons de répétitions et de points centraux comprises dans les combinaisons atteignant la puissance cible. Le diagramme ne contient pas les courbes dans les cas où les degrés de liberté sont insuffisants pour déterminer la signification statistique.
Examinez les valeurs sur la courbe pour déterminer l'importance de l'effet détectée par l'expérience à une valeur de puissance, un nombre de sommets et un nombre de points centraux spécifiques. La valeur de puissance 0,9 est généralement appropriée. Toutefois, certains spécialistes considèrent que la valeur 0,8 est adéquate. Si un plan offre une puissance inférieure, il se peut que vous ne puissiez pas détecter un effet significatif sur le plan pratique. L'augmentation du nombre de répétitions augmente la puissance du plan. Le nombre d'essais expérimentaux doit être suffisant dans le plan pour pouvoir atteindre la puissance adéquate. Un plan offre une plus grande puissance de détection d'un grand effet qu'un effet moins important.
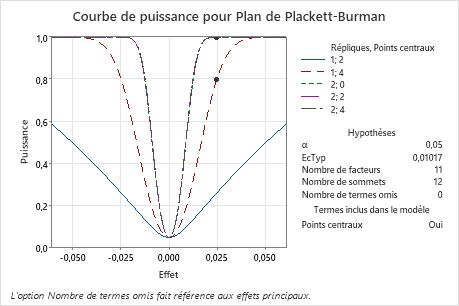
Dans ces résultats, Minitab calcule le nombre de répétitions pour atteindre une puissance cible d'au moins 0,8 ou 0,9 pour une importance d'effet de 0,025. L'expérience conçue comporte 12 sommets pour étudier 11 facteurs. Les calculs considèrent les expériences conçues avec 0, 2 ou 4 points centraux. La courbe montrant 1 répétition avec 4 points centraux présente un symbole pour l'effet de 0,25, où la puissance est supérieure à la puissance cible de 0,8. Les 3 courbes des expériences avec 2 répétitions présentent des symboles indiquant que la puissance de détection d'un effet de 0,025 est supérieure à la puissance cible de 0,9.
Comme il existe une solution avec 2 répétitions et 2 points centraux, ainsi qu'une solution avec 1 répétition et 4 points centraux, le diagramme inclut également une courbe pour une expérience avec 1 répétition et 2 points centraux. Puisque cette expérience n'atteint aucune des puissances cible pour l'effet de 0,025, cette courbe ne présente pas de symbole. Le diagramme n'inclut pas la courbe pour 1 répétition et 0 point central car cette expérience ne possède pas suffisamment de degrés de liberté pour déterminer la signification statistique lorsque 0 terme n'est omis dans le modèle.
