Sur ce thème
Calcul de la puissance
Formule
Ces calculs reposent sur une loi F avec un paramètre de non-centralité λ.
Paramètre de non-centralité
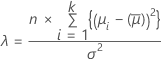
Puissance

Minitab calcule λ dans la pire hypothèse où toutes les autres moyennes sont à mi‑chemin entre les valeurs minimales et maximales. Le résultat est une configuration des moyennes qui minimise la puissance pour un effectif d'échantillon indiqué et une différence maximale spécifiée entre les moyennes.
Notation
| Terme | Description |
|---|---|
| k | nombre de niveaux |
| n | effectif de l'échantillon à chaque niveau |
| α | Seuil de signification |
| σ | Écart type |
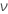 | degrés de liberté pour l'erreur, égaux à k * (n – 1) |
| fα | valeur critique (α supérieure pour une loi F avec k – 1 et ν degrés de liberté) |
| μi | réponse moyenne au niveau i |
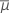 | 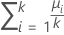 somme (μi)/k somme (μi)/k |
 | CDF de la loi F avec k – 1 degré de liberté du numérateur, v degrés de liberté du dénominateur et le paramètre de non-centralité λ, évaluée à fα |
Calcul de l'effectif de l'échantillon et de la différence maximale
Formule
Si vous indiquez des valeurs pour la puissance et l'effectif d'échantillon, Minitab calcule la valeur de différence maximale. Si vous indiquez des valeurs pour la puissance et la différence maximale, Minitab calcule la valeur de l'effectif d'échantillon.
Pour ces deux cas, Minitab utilise un algorithme itératif avec l'équation de puissance. A chaque itération, Minitab détermine la puissance pour l'effectif d'échantillon ou la différence d'un essai, et il s'arrête lorsqu'il atteint les valeurs indiquées.
Puissance cible et puissance réelle
Lorsque Minitab calcule l'effectif de l'échantillon, il peut déterminer qu'aucune valeur d'entier de l'effectif de l'échantillon ne génère la puissance cible. Dans de tels cas, Minitab affiche la valeur cible de la puissance à côté de la puissance réelle. La puissance réelle est la valeur d'entier de l'effectif de l'échantillon, la plus proche de la puissance cible, tout en lui étant supérieure.
