Sur ce thème
Niveau d'alpha
Le niveau de signification (dénoté par alpha ou α) est le niveau maximal acceptable du risque de rejet de l'hypothèse nulle lorsqu'elle est vraie (erreur de type I). Par exemple, si vous effectuez une ANOVA à un facteur contrôlé en utilisant les hypothèses par défaut, un α de 0,05 indique un risque de 5 % de conclure qu'une différence existe alors qu'il n'en existe pas.
Interprétation
Le seuil de signification permet de minimiser la valeur de puissance du test lorsque l'hypothèse nulle (H0) est vraie. Des valeurs plus élevées du seuil de signification donnent au test davantage de puissance, mais augmentent également les chances de faire une erreur de type I, c'est-à-dire de rejeter à tort l'hypothèse nulle alors qu'elle est vraie.
Ecart type supposé
L'écart type est la mesure la plus courante de la dispersion ou de la variabilité des données par rapport à la moyenne. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit.
Interprétation
L'écart type supposé est une estimation prévisionnelle de l'écart type de la population, que vous indiquez pour l'analyse de la puissance. Minitab utilise l'écart type supposé pour calculer la puissance du test. Des valeurs plus élevées de l'écart type indiquent une plus grande variation dans les données, ce qui diminue la puissance statistique d'un test.Différence maximale
La différence maximale est la différence qui existe entre la plus petite et la plus grande moyenne de groupe.
Interprétation
Si vous indiquez l'effectif de l'échantillon et la puissance, Minitab calcule la différence maximale. En général, des effectifs d'échantillons plus importants vous permettent de détecter une plus petite différence maximale à une puissance donnée.
- Avec 5 observations dans chaque groupe, la puissance du test est de 0,9 lorsque la différence est approximativement 4,4.
- Avec 7 observations dans chaque groupe, la puissance du test est de 0,9 lorsque la différence est approximativement 3,6.
- Avec 9 observations dans chaque groupe, la puissance du test est de 0,9 lorsque la différence est approximativement 3,1.
Pour examiner davantage la relation entre l'effectif de l'échantillon et la différence pouvant être détectée, utilisez la courbe de puissance.
Résultats
| Effectif d'échantillon | Puissance | Différence maximale |
|---|---|---|
| 5 | 0,9 | 4,42404 |
| 7 | 0,9 | 3,58435 |
| 9 | 0,9 | 3,09574 |
Puissance
La puissance d'une ANOVA à un facteur contrôlé est la probabilité selon laquelle le test déterminera que la différence maximale entre les moyennes des groupes est significative sur le plan statistique, lorsque cette différence existe réellement.
Interprétation
Si vous avez indiqué la différence et l'effectif d'échantillon maximaux, Minitab calcule la puissance du test. La valeur de puissance 0,9 est généralement appropriée. Une valeur de 0,9 indique que vous avez 90 % de chances de détecter une différence entre au moins deux des moyennes lorsqu'elle existe réellement dans les populations. Si un test a une faible puissance, vous pouvez ne pas réussir à détecter une différence et conclure à tort qu'il n'en existe aucune. En général, plus la différence ou l'effectif d'échantillon est faible, moins le test est puissant pour détecter une différence.
Par exemple, dans les résultats suivants, un effectif d'échantillon de 4 fournit une puissance d'approximativement 0,9 pour une différence maximale de 6, mais uniquement de 0,69 pour une différence maximale de 4. A chaque valeur de différence maximale, l'augmentation de l'effectif de l'échantillon augmente également la puissance du test.
Résultats
| Différence maximale | Effectif d'échantillon | Puissance |
|---|---|---|
| 2 | 4 | 0,206970 |
| 2 | 6 | 0,332203 |
| 2 | 8 | 0,454971 |
| 4 | 4 | 0,688630 |
| 4 | 6 | 0,909626 |
| 4 | 8 | 0,978713 |
| 6 | 4 | 0,968086 |
| 6 | 6 | 0,999226 |
| 6 | 8 | 0,999988 |
Courbe de la puissance
La courbe de puissance trace la puissance du test en fonction de la différence maximale entre la plus petite et la plus grande moyenne.
Interprétation
La courbe de puissance vous permet d'évaluer la puissance ou l'effectif d'échantillon adapté pour le test.
La courbe de puissance représente toutes les combinaisons de puissance et de différence maximale pour chaque effectif de l'échantillon lorsque le seuil de signification et l'écart type restent constants. Chaque symbole sur la courbe de puissance représente une valeur calculée en fonction des valeurs saisies pour deux propriétés. Par exemple, si vous entrez un effectif d'échantillon et une valeur de puissance, Minitab calcule la différence maximale correspondante et affiche la valeur sur le graphique.
Examinez les valeurs sur la courbe pour déterminer la différence maximale pouvant être détectée par le test à une puissance et un effectif d'échantillon spécifiques. La valeur de puissance 0,9 est généralement appropriée. Toutefois, certains spécialistes considèrent que la valeur 0,8 est adéquate. Si une ANOVA à un facteur contrôlé offre une puissance inférieure, il se peut que vous ne puissiez pas détecter une différence entre la plus petite moyenne et la plus grande moyenne lorsqu'il en existe réellement une.
Si vous augmentez l'effectif de l'échantillon, la puissance du test augmente également. L'échantillon doit contenir suffisamment d'observations pour atteindre une puissance adéquate. Toutefois, si l'effectif de l'échantillon est trop grand, vous risquez de gaspiller du temps et de l'argent sur un échantillonnage inutile ou de détecter des différences non significatives sur le plan statistique.
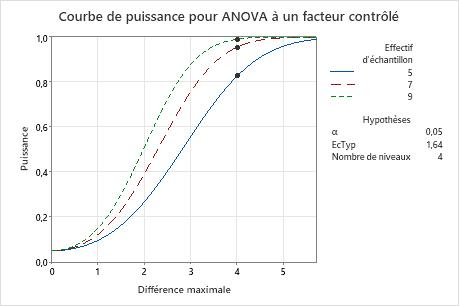
Dans ce graphique, chaque effectif de l'échantillon possède sa propre courbe. La courbe de puissance de l'effectif d'échantillon de 5 (dans chaque groupe) montre que le test offre une puissance d'approximativement 0,8 pour une différence maximale de 4. La courbe de puissance de l'effectif d'échantillon de 7 montre que le test offre une puissance d'approximativement 0,95 pour une différence maximale de 4. La courbe de puissance de l'effectif d'échantillon de 9 montre que le test offre une puissance proche de 1,0 pour une différence maximale de 4. Pour chaque courbe d'effectif d'échantillon, lorsque la différence maximale augmente, la puissance augmente également.
Effectif d'échantillon
L'effectif de l'échantillon correspond au nombre total d'observations dans l'échantillon.
Interprétation
Si vous indiquez la puissance et la différence maximale, Minitab calcule l'effectif d'échantillon nécessaire. L'effectif de l'échantillon correspond au nombre d'observations dans chaque groupe. Etant donné que les effectifs d'échantillons sont des nombres entiers, la puissance réelle du test peut être légèrement supérieure à la valeur de puissance que vous avez indiquée.
Si vous augmentez l'effectif de l'échantillon, la puissance du test augmente également. L'échantillon doit contenir suffisamment d'observations pour atteindre une puissance adéquate. Toutefois, si l'effectif de l'échantillon est trop grand, vous risquez de gaspiller du temps et de l'argent sur un échantillonnage inutile ou de détecter des différences non significatives sur le plan statistique.
Par exemple, les résultats suivants montrent que, pour une différence maximale de 4, un effectif d'échantillon plus important génère une plus grande puissance. Un effectif d'échantillon de 5 dans chaque groupe produit une puissance réelle d'environ 0,83, et un effectif d'échantillon de 6 produit une puissance réelle d'environ 0,91.
Résultats
| Différence maximale | Effectif d'échantillon | Puissance cible | Puissance réelle |
|---|---|---|---|
| 4 | 5 | 0,8 | 0,826860 |
| 4 | 6 | 0,9 | 0,909626 |
